Last update: 2012/07/01
[English] [Japanese]
更新履歴
はじめに
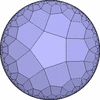
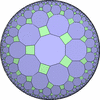
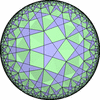
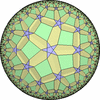
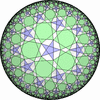
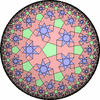
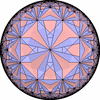
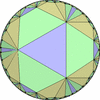
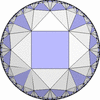
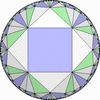
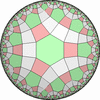
双曲平面一様充填形
一様充填形に関する話題
![[update]](update.png)
- 頂点図形が同じである複数の一様充填形
- "穴"の開いた一様充填形
- 特殊な頂点図形を持つ一様充填形
![[update]](update.png) (2012/07/01)
(2012/07/01)
- 複雑な形状を持つ変形一様充填形
- 複雑なユークリッド平面一様充填形
![[New]](new.png)
- 大二重斜方20・12面体とその仲間達
- 高次元の一様充填形
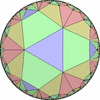
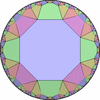
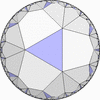
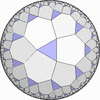
双曲平面一様充填形
(p,q,r) を基本とする一様充填形
内角が π/p,π/q,π/r (p,q,r は整数) であるような 球面/ユークリッド平面/双曲平面上の三角形 (p,q,r) を 基本とする一様充填形。 p,q,r 回の回転対称性を持つ。- (2,2,p) を基本とする一様充填形
(2,2,p) を基本とする一様充填形は 正多角柱(Prisms)または正多角反柱(Antiprisms) となります。




- (2,3,p) を基本とする一様充填形
(2,3,p) を基本とする一様充填形のうち、 (2,3,3), (2,3,4) または (2,3,5) を基本とするものは 一様多面体に、 (2,3,6) を基本とするものは ユークリッド平面一様充填形に、 それ以外 (2,3,p>=7) を基本とするものは双曲平面一様充填形に なります。- 一般的な凸な(convex)一様充填形
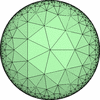

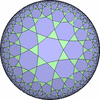



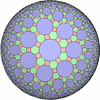
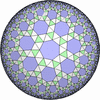
- 一般的な凸でない(non-convex)一様充填形



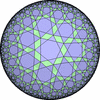

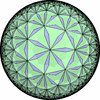




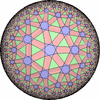

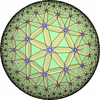



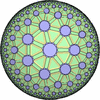
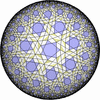
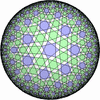
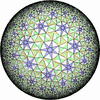

- (3,7,7/2) を基本とする凸でない(non-convex)一様充填形

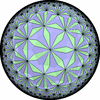


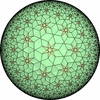

- 特殊な凸でない(non-convex)一様充填形


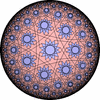

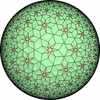

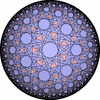

- 一般的な凸な(convex)一様充填形
- (2,p,q) を基本とする一様充填形
(2,p>=4,q>=4) を基本とする一様充填形のうち、 (2,4,4) を基本とするものは ユークリッド平面一様充填形に、 それ以外を基本とするものは双曲平面一様充填形になります。 - (p,q,r) を基本とする一様充填形
(p>=3,q>=3,r>=3) を基本とする一様充填形のうち、 (3,3,3) を基本とするものは ユークリッド平面一様充填形に、 それ以外を基本とするものは双曲平面一様充填形になります。
(p,q,r,...,s) を基本とする一様充填形
内角が π/p,π/q,π/r,...,π/s (p,q,r,...,s は整数) であるような 球面/ユークリッド平面/双曲平面上の多角形 (p,q,r,...,s) を 基本とする一様充填形。 p,q,r,...,s 回の回転対称性を持つ。記号は、独自の拡張 Wythoff 記号 を使っています。
- (p,q,r,s) を基本とする一様充填形
(p>=2,q>=2,r>=2,s>=2) を基本とする一様充填形のうち、 (2,2,2,2) を基本とするものは ユークリッド平面一様充填形に、 それ以外を基本とするものは双曲平面一様充填形になります。- 一般的な凸な(convex)一様充填形
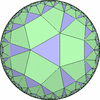
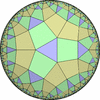


- 特殊な凸でない(non-convex)一様充填形
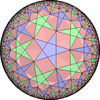
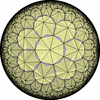
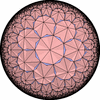

![[New]](new.png) (2012/07/01)
(2012/07/01)
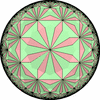
- 一般的な凸な(convex)一様充填形
- (p,q,r,s,...,t) を基本とする一様充填形
複合型の一様充填形
ユークリッド平面/双曲平面上には上記の様な多角形を基本としない "複合型" の一様充填形が存在します。 全て、変形面(snub faces)を持つ変形(snub)一様充填形です。 また、たった一つのユークリッド平面上の特殊な一様充填形を除き、 全て凸な(convex)一様充填形です。記号は、独自の拡張 Wythoff 記号 を使っています。
- |p q (r|s)
頂点図形が [p,3,q,3,2*s,r,2*s,3] である様な一様充填形。 |p q * と * r|s の2種類のタイプの ものが複合した一様充填形です。- 一般的な凸な(convex)一様充填形
このタイプには、 ユークリッド平面上にも一つだけ一様充填形があります。

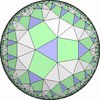
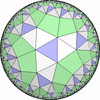
- 特殊な凸でない(non-convex)一様充填形
![[update]](update.png)
このタイプには、 ユークリッド平面上に、9つの 凸でない(non-convex)一様充填形があります。
![[3,3,3,4,4]](complex/s-22+2-2r_s.png)
![[3/2,Inf,3/2,Inf,3/2,4,4]](complex/sisrint_s.png)
![[3/2,Inf,3/2,Inf,3/2,4/3,4/3]](complex/gisrint_s.png)
![[3/2,Inf,3/2,Inf,3/2,12/5,6,12/5]](complex/sisstdobhint_s.png)
![[3/2,Inf,3/2,Inf,3/2,12/7,6/5,12/7]](complex/gisstdobhint_s.png)
![[3/2,Inf,3/2,Inf,3/2,12,6/5,12]](complex/sisdochint_s.png)
![[3/2,Inf,3/2,Inf,3/2,12/11,6,12/11]](complex/gisdochint_s.png)
![[3/2,Inf,3/2,4/3,4/3,3/2,4/3,4/3]](complex/sisdirint_s.png)
![[3/2,Inf,3/2,4/3,4/3,3/2,4,4]](complex/gisdirint_s.png)
- 一般的な凸な(convex)一様充填形
- |p q r|s
頂点図形が [p,3*s,q,3*s,r,3*s] である様な一様充填形。 変形面(snub faces)が(通常の三角形ではなくて) 3*s 角形であるような一様充填形です。 - p|(|q r s)
頂点図形が p*[q,3,r,3,s,3] である様な一様充填形。 一様充填形 |q r s (頂点図形が [q,3,r,3,s,3]) を、 頂点の周りで p 回 繰り返した形です。 - |p (q r|)
頂点図形が [p,4,2*q,2*r,4] である様な一様充填形。 正方形を変形面(snub faces)とする変形(snub)充填形の一種です。 - さらに複雑なもの
上記のタイプを複合させて、さらに複雑な一様充填形を 構築する事が出来ます。 特に、複数種類の変形面(snub faces)を持つものは、 一般形を記号で記述することすら困難です。- 一般的な凸な(convex)一様充填形
- 特殊な凸でない(non-convex)一様充填形
![[New]](new.png)
このタイプには、 ユークリッド平面上に、4つの 凸でない(non-convex)一様充填形があります。
![[3/2,Inf,3/2,4,4,3/2,4/3,4/3]](complex/irsint_s.png)
![[4,Inf,4/3,8/3,4,8/3]](complex/irstobsint_s.png)
![[4,Inf,4/3,8,4/3,8]](complex/irocsint_s.png)
![[4,Inf,4/3,8/3,8]](complex/sirostobint_s.png)
![[4,Inf,4/3,8,8/3]](complex/girostobint_s.png)
- 一般的な凸な(convex)一様充填形
since 2002/10/18