- Wythoff 型 ではない。
- 頂点に 8 個もの面が集まる(他の一様多面体は最大 6 個)
- 変形面である正方形を持つ。
- 大二重斜方20・12面体 |3 5/2 3/2 5/3
正方形を変形面とする一様多面体である、 大二重斜方20・12面体(Great Dirhombicosidodecahedron)。 大二重変形二重20・12面体(Great Disnub Disicosidisdodecahedron)とも。 別名、Miller's Monster。
大二重斜方20・12面体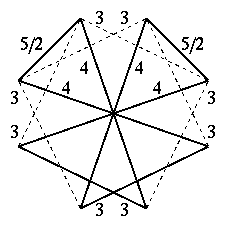
頂点図形
- 大二重変形二重斜方12面体 (Skilling's Figure)
Skilling がコンピュータを使って 1975 年に発見した 大二重変形二重斜方12面体(Great Disnub Dirhombidodecahedron)。 別名、Skilling's Figure。 一様多面体のほとんどの条件を満たしますが、 4つの面が重なる辺があるので通常は一様多面体には数えません。
大二重変形二重斜方12面体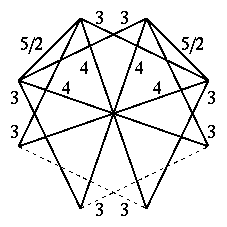
頂点図形
- 大変形20・12・12面体 |3 5/2 5/3
正3角形を変形面とする一様多面体である、 大変形20・12・12面体(Great Snub Icosidisdodecahedron)。 鏡像異性体があります。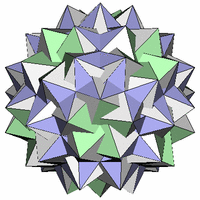
大変形20・12・12面体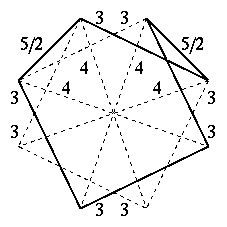
頂点図形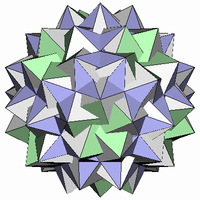
大変形20・12・12面体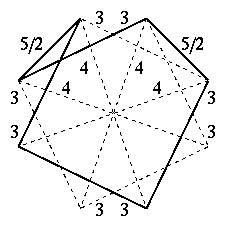
頂点図形
- 20個の正8面体の複合形
一様複合多面体である 20個の正8面体の複合形(Compound of 20 Octahedra)。
20個の正8面体の複合形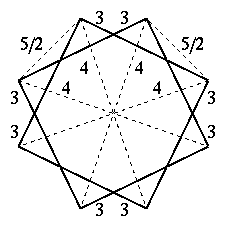
頂点図形
- 20個の4面半6面体の複合形
一様複合多面体である 20個の4面半6面体の複合形(Compound of 20 Tetrahemihexahedra)。 鏡像異性体があります。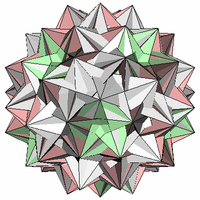
20個の4面半6面体の複合形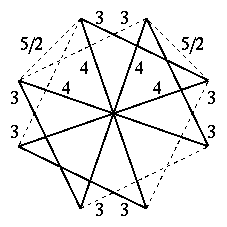
頂点図形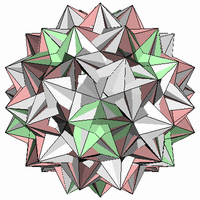
20個の4面半6面体の複合形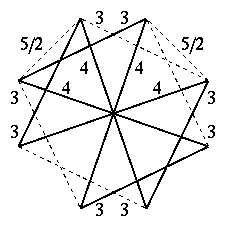
頂点図形
このページへのお問い合わせは
hsaka@mth.biglobe.ne.jp
まで御願いします。