はじめに
→ トップページへ戻る一様充填形(Uniform Tessellation)とは
- 正多面体とアルキメデスの立体
正多面体(Regular Polyhedra) が以下の5種類あることは、プラトンの時代から良く知られており、 プラトンの立体(Platonic solids)とも呼ばれます。

正4面体
{3,3}
立方体
(正6面体)
{4,3}
正8面体
{3,4}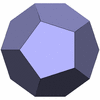
正12面体
{5,3}
正20面体
{3,5}正多面体は、頂点形状が全て同じであり面が一種類の正多角形で 構成されているという特徴を持っています。 その条件を少し緩めて、頂点形状が全て同じだが複数種類の正多角形に より構成された多面体をアルキメデスの立体(Archimedean solids) といい、正多角柱(Prisms)と正多角反柱(Antiprisms) を除くと以下の13種類があります。
(補足)
アルキメデスの立体は準正多面体(Quasi-regular Polyhedra) とも呼ばれますが、準正多面体という言葉の定義が揺れているので ここでは使いません。 また、図形の名前も揺れがありますが、 ここでは『多面体の模型』に従いました。
切頭4面体
[3,6,6]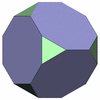
切頭6面体
[3,8,8]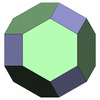
切頭8面体
[4,6,6]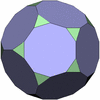
切頭12面体
[3,10,10]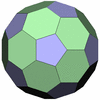
切頭20面体
[5,6,6]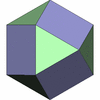
立方8面体
[3,4,3,4]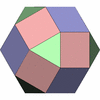
斜方立方8面体
[3,4,4,4]
20・12面体
[3,5,3,5]
斜方20・12面体
[3,4,5,4]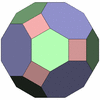
斜方切頭立方8面体
[4,6,8]
変形立方体
[3,3,3,3,4]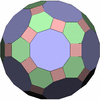
斜方切頭20・12面体
[4,6,10]
変形12面体
[3,3,3,3,5] - 星型正多面体と一様多面体
次に、上記の多面体は全て凸(convex)な多面体でしたが、 凸という条件を省いて、頂点形状が星形になったり星形多面体により 構成されていても良いとすると、 正多面体はさらに以下の4種類が追加され、これらの美しい多面体は 星形正多面体(Stellated Regular Polyhedra)または ケプラー・ポワンソの立体(Kepler & Poinsot's solids)と 呼ばれています。

大12面体
{5,5/2}
小星形12面体
{5/2,5}
大20面体
{3,5/2}
大星形12面体
{5/2,3}結局、正多面体(Regular Polyhedra)は、最初に上げた凸な プラトンの立体と星形のケプラー・ポワンソの立体を合わせた9種類と なります。
また、アルキメデスの立体も同様の拡張が可能で、 さらに53種類も追加されます。 そして、これら75種類(5+13+4+53種類)の多面体の総称を 一様多面体(Uniform Polyhedra) といいます。 一様多面体については、美しい立体も多く、 いろいろなのサイトで紹介されていますので、是非眺めてみてください。
- 正充填形とアルキメデスの充填形
頂点の周りに、正3角形を3、4または5個集めると 頂点角の和が 360°に満たないので正多面体になりますが、 正3角形を6個集めた場合は、頂点角の和が 360°になり、 良く知られている様にユークリッド平面を覆う 正充填形(Regular Tessellation)となります。 同様に、正方形を4個、正6角形を3個集めた場合も充填形になります。

{3,6}
{4,4}
{6,3}これらの正充填形から、正多面体に対するアルキメデスの立体と同様のものが、 以下の8種類考えられてアルキメデスの充填形と呼ばれます。
![[3,6,3,6]](ue2/2-36_s.png)
[3,6,3,6]![[3,12,12]](ue2/23-6_s.png)
[3,12,12]![[3,4,6,4]](ue2/36-2_s.png)
[3,4,6,4]![[4,6,12]](ue2/236_s.png)
[4,6,12]![[3,3,3,3,6]](ue2/s-236_s.png)
[3,3,3,3,6]![[4,8,8]](ue2/24-4_s.png)
[4,8,8]![[3,3,4,3,4]](ue2/s-244_s.png)
[3,3,4,3,4]![[3,3,3,4,4]](ue2/s-22+2-2_s.png)
[3,3,3,4,4]さらに、一様多面体と同様な凸でない場合(平面に凸凹があるかどうかは? ですが)の充填形も構築可能で、 ユークリッド平面一様充填形(Uniform Tessellations on the Euclid Plane) と呼ばれます。 なお、ユークリッド平面には星形正充填形はありません。
(補足)
Uniform Tessellations を『一様充填形』と訳したのは私の勝手な訳です。 もしかすると、別の訳語があるのかもしれません。 - 双曲平面の正充填形と双曲平面の一様充填形
では、正3角形を7個集めた場合や正方形を5個集めた場合は どうでしょうか。 頂点角の和が 360°以上になるために、通常のユークリッド空間では そうした図形は構築できません。 しかし、数学的にそうした図形が成り立つ様な空間自体が定義できて 双曲空間(Hyperbolic Space)と呼ばれます。 この場合は2次元ですから、双曲平面(Hyperbolic Plane)となります。 この平面上では、頂点の周りに任意の正多角形を任意個集めた図形が構築可能で 双曲平面正充填形(Regular Tessellation on the Hyperbolic Plane) と呼ばれます。
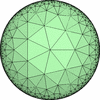
{3,7}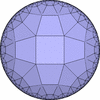
{4,5}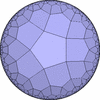
{5,4}
{7,3}また、双曲平面上には星形の正充填形も存在します。 そして、一様多面体と同様な複数種類の正多角形からなる充填形も構築可能で、 双曲平面一様充填形(Uniform Tessellations on the Hyperbolic Plane) と呼ばれます。
しかしながら、この双曲平面一様充填形はあまり研究されてないようで、 Web 上でもほとんど情報が無いので、 このサイトを作ってみました。 綺麗な図形も多いので、是非眺めてみてください。
一様充填形を表す記号(Wythoff 記号)
- Wythoff 記号
一様多面体は(多少の揺れがあるとはいえ)全て名前が与えられていますが、 一様充填形は、ほとんど名前が与えられていない様です。 そのため、記号で表すこととしました。 一様充填形(一様多面体)を表す記号としては、以下のようなものがあります。
- Schläfli の記号
一般的に、正充填形(正多面体)は {p,q} と表されます。 これは頂点に正 p 角形が q 個集まっていることを示します。 そして、一様充填形(一様多面体)は正充填形(正多面体)の頂点を 切り飛ばした(faceted)ものと考えることで、 例えば、切頭8面体は t{3,4} の様に表されます。 この方法を拡張することで、一様多面体は(一種類を除き) 全て表すことが出来ます。 しかし、一様充填形の中には正充填形と無関係であるものが あるためこの方法は使えません。 - 頂点形状
正4面体なら [3,3,3]、立方8面体なら [3,4,3,4] という様に、 頂点に集まる多角形を順に記述する方法もあります。
この方法だと、全ての一様充填形を表すことが可能です。 しかし、一様充填形の中には同じ頂点形状を持ちながら 別種の一様充填形であるものもあります。 また、対称性があらわには分からないので、分類等に不便です。
結局、上記の方法はどちらも欠点があるので、 Wythoff 記号を使用することとしました。 Wythoff 記号は、内角が π/p,π/q,π/r (p,q,r は整数) であるような双曲平面(球面、ユークリッド平面)上の三角形 (p,q,r) を基本として一様充填形(一様多面体)を表すものです。 この三角形 (p,q,r) は回転および鏡像操作により双曲平面を覆いつくします。そして、任意の双曲平面上の三角形を基本とする全ての一様充填形を 構築する事ができ、構築された一様充填形を Wythoff 型 (Wythoffian) と言います。 頂点が三角形のどの位置に来るかによって、 以下の4つのタイプの分類されます。
- p|q r
頂点が三角形 PQR (P,Q,R の内角はそれぞれ π/p,π/q,π/r) の頂点 P にある場合です。 頂点 P の周りに正 q 角形と正 r 角形が交互に p 回繰り返す 頂点形状 p*[q,r] となります。 なお、q または r が 2 である場合は正充填形(正多面体)となります。
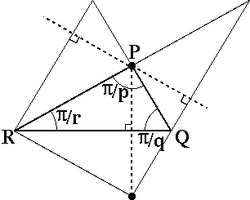
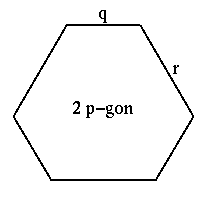
三角形 PQR と頂点位置 頂点図形 - p q|r
頂点が三角形 PQR (P,Q,R の内角はそれぞれ π/p,π/q,π/r) の辺 PQ 上にある場合です。 正確には点 R から ∠PRQ' の二等分線を引き、辺 PQ と交差した 位置に頂点がある場合です。 正 p 角形と正 q 角形が正 2*r 角形でつながれた 頂点形状 [p,2*r,q,2*r] となります。 なお、p または q が 2 である場合は正充填形(正多面体)の 頂点を切り飛ばした形(切頭型)となります。
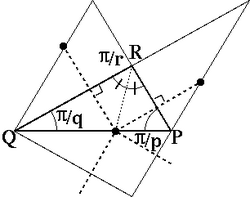
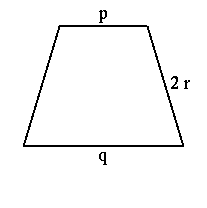
三角形 PQR と頂点位置 頂点図形 - p q r|
頂点が三角形 PQR (P,Q,R の内角はそれぞれ π/p,π/q,π/r) の内心にある場合です。 正 2*p 角形、正 2*q 角形と正 2*r 角形がつながった 頂点形状 [2*p,2*q,2*r] となります。
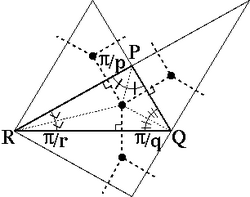
三角形 PQR と頂点位置 頂点図形 - |p q r
頂点が三角形 PQR (P,Q,R の内角はそれぞれ π/p,π/q,π/r) の内部にある場合ですが、 頂点は一つおきの三角形にしかありません。 正 p 角形、正 q 角形と正 r 角形が3つの正3角形で つながれた頂点形状 [p,3,q,3,r,3] となります。 変形(snub)充填形(変形多面体)と呼びます。
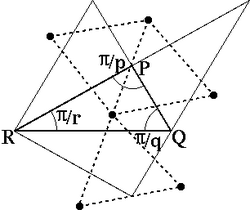
三角形 PQR と頂点位置 頂点図形
さらに、三角形 PQR の外側に頂点が来る場合に、 以下の2タイプの凸でない一様充填形が構築できます。
- p q/(q-1)|r/(r-1)
p q|r の拡張型で、 頂点が三角形 PQR (P,Q,R の内角はそれぞれ π/p,π/q,π/r) の辺 PQ の延長線上にある場合です。 正確には点 R から ∠P'RQ の二等分線を引き、 辺 PQ の延長線上と交差した 位置に頂点がある場合です。 正 p 角形と正 q/(q-1) 角形が正 2*r/(r-1) 角形でつながれた 頂点形状 [p,2*r/(r-1),q/(q-1),2*r/(r-1)] となります。
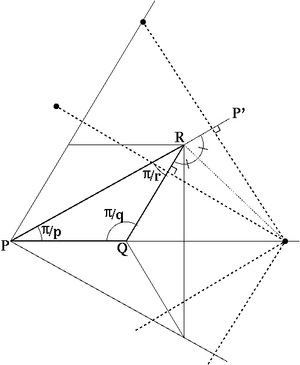
三角形 PQR と頂点位置 - p q/(q-1) r/(r-1)|
p q r| の拡張型で、 頂点が三角形 PQR (P,Q,R の内角はそれぞれ π/p,π/q,π/r) の外心にある場合です。 正 2*p 角形、正 2*q/(q-1) 角形と正 2*r/(r-1) 角形がつながった 頂点形状 [2*p,2*q/(q-1),2*r/(r-1)] となります。
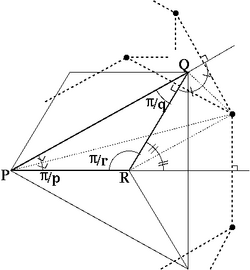
三角形 PQR と頂点位置
また、Wythoff 記号は、内角が π/p',π/q',π/r' (p',q',r' は有理数) である様な双曲平面上の三角形にも適用できます。 ただし、この場合の三角形は、p,q,r が整数である三角形 (p,q,r) を 複数個組み合わせたものである必要があります。 そうでない場合は、双曲平面を有限個数で覆うことが出来ないため、 一様充填形を構築できません。 また、組み合わせの数は、双曲平面を覆う回数と等しく、 その数が導かれた一様充填形の密度(density)となります。
- Schläfli の記号
- 拡張 Wythoff 記号
Wythoff 記号は双曲平面上の三角形を基本とする一様充填形にしか 適用できません。 しかし、双曲平面上には四角形以上の多角形を基本とする一様充填形や 多角形を基本としない一様充填形が存在します。 そこで、独自の拡張 Wythoff 記号を考案しました。
補足
まず、内角が π/p,π/q,π/r,...,π/s (p,q,r,...,s は整数) である任意の双曲平面上の多角形を基本とする一様充填形は、 三角形を基本とするものに準じて以下の4つのタイプに分類され、 各々に拡張 Wythoff 記号を考案しました。
同様の拡張 Wythoff 記号を考案した方もおられます [www.hadron.org/~hatch/HyperbolicTesselations/] が、オリジナルの Wythoff 記号と互換性がないため混乱しそうなので 使用しませんでした。- p|q s|r ...
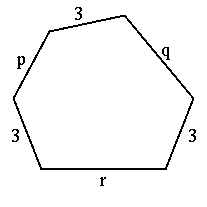
頂点が多角形 PQR...S (P,Q,R,...,S の内角はそれぞれ π/p,π/q,π/r,...,π/s) の頂点 P にある場合です。 頂点 P の周りに、正 2*r,... 角形でつながれた 正 q 角形と正 s 角形が交互に p 回繰り返す 頂点形状 p*[q,2*r,...,s,...,2*r] となります。
- p q|r ... s
頂点が多角形 PQR...S (P,Q,R,...,S の内角はそれぞれ π/p,π/q,π/r,...,π/s) の辺 PQ 上にある場合です。 正確には点 R,...,S から各々の内角の二等分線を引き、 辺 PQ と交差した位置に頂点がある場合です。 正 p 角形と正 q 角形が正 2*r,...,2*s 角形でつながれた 頂点形状 [p,2*s,...,2*r,q,2*r] となります。
- p q r ... s|
頂点が多角形 PQR...S (P,Q,R,...,S の内角はそれぞれ π/p,π/q,π/r,...,π/s) の内心にある場合です。 正 2*p,2*q,2*r,...,2*s 角形がつながった 頂点形状 [2*p,2*q,2*r,...,2*s] となります。
- |p q r ... s
頂点が N 角形 PQR...S (P,Q,R,...,S の内角はそれぞれ π/p,π/q,π/r,...,π/s) の内部にある場合ですが、 頂点は一つおきの N 角形にしかありません。 正 p,q,r,...,s 角形が N 個の正 N 角形で つながれた頂点形状 [N,p,N,q,N,r,N,...,N,s] となります。 変形(snub)充填形です。
補足
大二重斜方20・12面体 も同様の拡張 Wythoff 記号を使って、|3 5/2 3/2 5/3 と表される、4個の正方形による変形多面体ですが、 ここで述べたものとは少し違います。
これらの拡張 Wythoff 記号は、 内角が π/p',π/q',π/r',...,π/s' (p',q',r',...,s' は有理数) である様な双曲平面上の多角形にも 適用できますが、この場合の多角形は、p,q,r,...,s が整数である 多角形 (p,q,r,..,s) を複数個組み合わせたものである必要があります。 ただし、現在のところ、こうした多角形による一様充填形は わずか4個しか見つけていません。 また、すべて三角形が組み合わさった多角形を基本とするものです。
- p|q s|r ...
- 拡張 Wythoff 記号(その2)
次に、双曲平面上の多角形を基本としない "複合型" の一様充填形 に対する拡張 Wythoff 記号を説明します。
- |p q (r|s)
頂点図形が [p,3,q,3,2*s,r,2*s,3] である様な一様充填形。 |p q * と * r|s の2種類のタイプの ものが複合した一様充填形です。
一般に |(p1|q1 ...) (p2|q2 ...) ... (pN|qN ...) と拡張できて、この場合の頂点図形は、 [...,2*q1,p1,2*q1,..., N, ...,2*q2,p2,2*q2,..., N, ..., ...,2*qN,pN,2*qN,..., N] です。 - |p q r|s
頂点図形が [p,3*s,q,3*s,r,3*s] である様な一様充填形。 変形面(snub faces)が(通常の三角形ではなくて) 3*s 角形であるような一様充填形です。
一般に |p1 p2 ... pN|s と拡張できて、この場合の頂点図形は、 [p1,N*s,p2,N*s,..,N*s,pN,N*s] です。 - p|(|q r s)
頂点図形が p*[q,3,r,3,s,3] である様な一様充填形。 一様充填形 |q r s (頂点図形が [q,3,r,3,s,3]) を、 頂点の周りで p 回 繰り返した形です。
一般に p|(|q1 q2 ... qN) と拡張できて、この場合の頂点図形は、 p*[q1,N,q2,N,..,N,qN,N] です。 - |p (q r|)
頂点図形が [p,4,2*q,2*r,4] である様な一様充填形。 正方形を変形面(snub faces)とする変形(snub)充填形の一種です。
一般に |p1 p2 ... pN-1 (q r ...|) と拡張できて、この場合の頂点図形は、 [p1,2*N,p2,2*N,..,2*N,pN-1,2*N,2*q,2*r,...,2*N] です。
上記のタイプを複合させて、さらに複雑な一様充填形を 構築する事が出来ます。 特に、複数種類の変形面(snub faces)を持つものは、 一般形を記号で記述することすら困難です。
- |p q (r|s)
![[update]](update.png)