さて、各手法の賭け方がわかりました。
どの手法を使っても期待値が同じになることも確認しました。
でも、実際にプレーすると、儲かる人もいれば、損をする人がいます。
その謎を解明していきましょう。
これは、実際にプレーしてみるしかありません。
でも、本当に4000人のプレーヤーにお願いして、1000回も同じ賭け方を延々と繰り返してもらうのは大変。
そこで、コンピュータ上でシミュレーションします。
コンピュータに、4種類の手法をそれぞれ1000人のプレーヤーが1000回繰り返した場合と同じことをしてもらうわけです。
エクセルの関数機能とマクロ機能を使えば、簡単にできますね。
その数字に基づいて書かれたのが、先に紹介した広告メールの内容なんです。
広告メールの内容にウソはない、というのはこういうことだったのです。
|
賭け方 |
1回あたり収支 |
| 手法A |
1つの数字にだけ毎回10ドルを賭ける。 |
当たると350ドル、外れると-10ドル。 |
| 手法B |
10個の数字にそれぞれ1ドルずつ賭ける。 |
どれかが当たると26ドル、外れると-10ドル。 |
| 手法C |
赤黒どちらかに毎回10ドルを賭ける。 |
当たると10ドル。外れると-10ドル。 |
| 手法D |
赤黒に5ドル、奇数偶数に5ドルを賭ける。 |
両方当たると10ドル、両方外れると-10ドル。
一方が当たると0ドル。 |
これらの手法、、期待値を計算すると、どの手法も同じ「−.0.526ドル」でした。
これは1回あたりの期待値なので、1000回あたりの期待値は、「−526ドル」ということになります。
実際にシミュレーションした結果はどうなったかというと、以下の通りです。
<1000回実行後の収支平均>
| 手法A |
手法B |
手法C |
手法D |
| −485$ |
−508$ |
−515$ |
−524$ |
それぞれの手法を1000人の人が1000回繰り返したので、その1000人の平均値です。
あれ?
計算上の期待値は「−526ドル」のはずですが、様子が変ですね。
手法Dは「−524ドル」で、ほぼ計算通りです。
でも、手法Aは、「−485ドル」と、ずいぶん理論値と違いがあります。
しかも、手法D→手法C→手法B→手法Aといくにつれて、理論値との開きが大きくなっています。
これはどういうこと?
この謎を解くには、1000人全体がどんな収支結果だったかを見てみる必要があります。
では、手法Aの1000人がどんな収支結果だったかをグラフにしてみましょう。
−8000ドルから8000ドルまで、100ドル刻みで人数を集計して棒グラフにすると、以下のようになります。
<手法A1000人の収支結果>
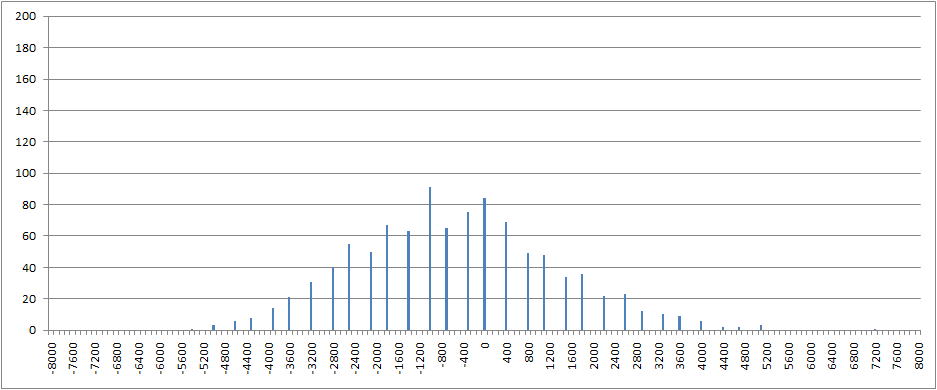
横軸は、最終的な収支金額(100ドル刻みで集計)。
縦軸は人数です。
−500ドル付近を頂点に、山形を形成しているのがわかります。
−500ドル付近というのは、計算上の期待値「−526ドル」のこと。
この周辺が一番人数が多いのですが、その期待値から離れるにつれて人数が少なくなっていきます。
計算上の期待値が「−526ドル」といっても、全員がドンピシャリその値になるということではありません。
その前後にいろんな金額の人たちが存在して、平均すると期待値に近い数字になるということです。
世の中には運のいい人悪い人がいますから、このように結果はばらけてしまうというわけです。
コンピュータシミュレーションでも、ちゃんと運の善し悪しが再現されてますね。
でも、実は、手法Aの特徴は、これだけを見ていたのではわかりません。
他の手法と比べることで特徴がはっきりします。
特に、手法Dと比較すると、驚くべきことが、はっきりしてきます。
次に手法Dの収支結果を見てみましょう。
 
|