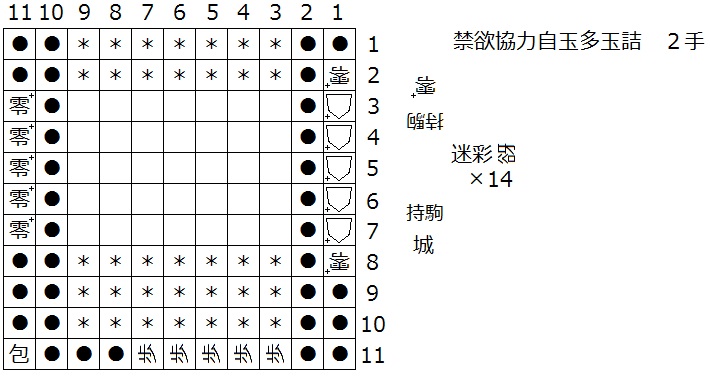
ルール:禁欲協力自玉多玉詰(11×11盤) 2手 (特殊ルールの説明)
*13〜17地点の白抜きの駒は受方の覆面駒で、その種類は通常駒および城、包(Pao)、零、谺のいずれかとします。
*「*」印は「駒を打つことのできない地点」を表します(元からその地点に駒があったり、通過ないし移動するのは可能)。
*初形において、盤面(「*」地点を含む空きマス)あるいは攻方か受方の持駒に、合計14枚の迷彩中立駒の谺が存在します。
(「Web Fairy Paradise」112号掲載、2017年10月)

ルール:禁欲協力自玉多玉詰(11×11盤) 2手 (特殊ルールの説明)
*13〜17地点の白抜きの駒は受方の覆面駒で、その種類は通常駒および城、包(Pao)、零、谺のいずれかとします。
*「*」印は「駒を打つことのできない地点」を表します(元からその地点に駒があったり、通過ないし移動するのは可能)。
*初形において、盤面(「*」地点を含む空きマス)あるいは攻方か受方の持駒に、合計14枚の迷彩中立駒の谺が存在します。
(「Web Fairy Paradise」112号掲載、2017年10月)
特殊ルール詰将棋を扱うインターネット配信誌「Web Fairy Paradise」で発表した作品です。
同誌で解答募集した出題図は上記の通りですが、実はこの出題図は以下の要領で一般化することができます。
下記のパラメータで定まる出題図を「(N,L,n)型」と呼ぶことにすると、上記の出題図は(11,7,14)型に相当します。
これは盤面のサイズ N が最小の場合に相当します。
(なお、本作が成立するためには後述の通りパラメータ N,L,n が「ある条件」を満たす必要がありますが、(11,7,14)型は実際にその条件を満たしています。)
(p,q)をパラメータの条件(#)に現れる整数の組とするとき、「(p+3,N-1-q)城、(1,N-1-q)→(p+3,N-1-q)△+」まで。
例えば上記出題図の(N,L,n) = (11,7,14)の場合には、「(5,3)城、(1,3)→(5,3)△+」まで。
上記の解答にある、持駒の城の正しい打ち場所を知るためには、パラメータの条件(#)に現れる整数の組(p,q)を知る必要があり、そのためにはパラメータ n を素因数分解する必要があります。
このように、「素因数分解の計算をしないと解けない詰将棋」を創りたかった、というのが本作の出発点です。
ご存知の方もおられるでしょうが、巨大な整数の素因数分解は、(少なくとも本作の出題時点では)最新鋭のコンピュータを使ってもなお膨大な時間が必要となる難しい種類の計算であり、そのことがある種の暗号技術の安全性の根拠となっています。
この素因数分解に比べると、二つの整数の掛け算はとても簡単な種類の計算です。
そこで、巨大な(しかし、掛け算すらできないほど巨大ではない)素数 p と q を選び、 n = p × q を計算し、それに従って残りのパラメータ N と L を条件(#)が成り立つように適切に選ぶことで、「作った(パラメータを選んだ)本人以外には解答を得ることが(事実上)不可能な詰将棋」ができます。
折角(?)暗号の研究をしている身なので、暗号っぽい要素を持った詰将棋を創ってみたいなあ、というのが本作の狙いでした。
ちなみに、こんな奇々怪々な作品でも、出題時にはちゃんと(作者本人以外の)正解者が現れました。
ありがたいことです。
なお、前述の解答手順で実際に詰みとなっていることを確認するのにも少々の考察を要します。 詳細は後述することにして、ここでは概要だけ説明します。
以降では、本作が完全作である、つまり作意手順はちゃんと詰んでいる一方で他の手順では詰まないということを証明します。 かなり長いです。
最初にいくつかの事実を注意しておきます。
まず、 a = 3 とすると、
『初形で迷彩中立谺がすべて攻方の持駒で、(1,b)△+が城または包である』という配置は上記の手順と整合性があります。 (受方は2手目の時点で駒を取らずに王手を回避できないので、2手目の駒取りは禁欲ルールに反しません。) そして、この可能性『 』においては、2手目が(N,b)零+への逆王手であるものの、それは攻方が(N-2,b)中立谺と打って回避できます。 つまり、この初手および2手目と整合性があるが2手目で攻方が詰みとならないような、覆面駒の種類および迷彩駒の配置の可能性が存在するため、この手順で攻方が詰んでいるとは確定しません。 よって a = 3 の場合には、今考えている手順は逃れとなります。
a ≧ 4 のとき、2手目のような動きが可能な△+は、包あるいは、盤面の別の包から中立谺たちを経由して包の利きを与えられた谺のいずれかに限られます。 ここで、事実1の帰結2.より、もし1筋の別の△+が包であったとしても、その包が利きを伝えることのできる中立谺は存在しません。 このことから、2手目で動いた(1,b)の△+が谺である可能性は無くなり、その駒は包に確定します。
2手目「 (1,b)→(a,b)△+ 」を指せているからには、この手は受方自身に王手を掛ける手ではありません。
このことから、 a 筋において、 b 段目よりも上側と b 段目よりも下側には、それぞれ中立谺が多くても1枚までしか存在しません。
(2枚以上存在すると、 b 段目から遠い方の中立谺が2手目の後の時点で包の利きを得て、(a,b)の包+に逆に王手を掛けてしまいます。)
また、事実1の帰結2.より b 段目には中立谺は存在しません。
これらのことから、初手の後の時点で(a,b)の城から中立谺に利きが伝わっている可能性はありません。
これと事実1を合わせると、初手の後の時点で中立谺の各々は、利きを持たないか歩の利きになっているかのいずれかに限られます。
さて、2手目は駒取りであり、禁欲ルール下でその手を指せているからには、初手に対して受方には駒を取らない応手が不可能であったということになります。 特に、2手目に受方は、 b 段目の3筋から a-1 筋までのいずれかの地点に持駒の零+を打って王手を回避することができなかった、ということになります。
仮に2手目に受方がそれらの地点に零+を打ったとして、その後の、攻方に手番が移った状況を考えてみます。
上の考察により、この時点で盤面の城または包(1筋の覆面駒がそれらの駒である場合を含む)が中立谺に利きを伝えていることはあり得ません。
また、2手目に打った零+と攻方の城の位置関係から、攻方の城が1筋のロイヤル駒に直接王手を掛けていることもあり得ません((a,b)城から(2,b)石を跳び越えて(1,b)△+へ、という利きは零+が遮っています)。
つまり、もし上記の地点に零+を打てたならば、受方は2手目に駒を取らずに王手を防げたはずです。
しかし実際には上記の通り、(2手目に駒取りを指せたことから)受方は2手目に駒を取らずに王手を防げなかったので、受方は2手目に上記の地点に零+を打つこと自体ができなかったことになります。
この零+を打てなかった理由として考えられるものは、
(*) 上記の地点に零+を打ったとすると、その後に攻方に手番が移った際、その零+に対する攻方の利きが存在し、2手目が受方の王手放置になるという場合に限られるので、上記(*)が成立していることが確定します。
一方、前述の通り、このように零+を打った後で攻方に手番が移った状況では、中立谺の各々は利きを持たないか攻方の歩の利きになっているかのいずれかです。 このことから、上記(*)のような可能性が生じるのは、以下の状況に限られます。
(**) 3 ≦ k ≦ a-1 をみたすどの k についても、(k,N)地点が石ではなく中立歩であり、 k 筋の b+1 段目から N-1 段目までの地点がすべて中立谺で埋まっている(実際、上記(**)のように中立谺が配置されていると、攻方の手番の際には、 k 筋の N 段目の中立歩の利きが k 筋の N-1 段目から b+1 段目までの中立谺へ順に伝わり、 b+1 段目の中立谺が攻方歩の利きを与えられ、そのことで(k,b)地点への利きが生じます。) したがって、2手目「 (1,b)→(a,b)△+ 」を指せたという事実から、初形における迷彩中立谺の配置は上記(**)を満たすことが確定します。
ここで、初形における覆面駒の種類と迷彩中立駒の配置が、
『(1,b)△+が包、それ以外の△+は包でも城でもない何らかの駒であり、上記(**)のように3筋~ a-1 筋、 b+1 段目~ N-1 段目の長方形の領域がすべて中立谺で埋まっており、残りの中立谺はすべて攻方の持駒にある』を満たしている場合を考えます。 このとき、初手「 (a,b)城 」の後で受方に手番が移った状況では、 N 段目の中立歩は「受方の」歩の利きになっており、これらの駒から盤面の中立谺に利きが伝わることはありません。 今、盤面の中立谺はそれ以外の駒から利きを与えられている可能性もありませんので、この時点で盤面の中立谺はどれも利きを持っていません。 すると、受方が駒を取らずに(a,b)の城からの王手を回避する手段は、 b 段目の3筋~ a-1 筋のいずれかの地点に(1,b)△+を動かすか持駒の零+を打つ以外に存在しませんが、前述の通り、攻方の手番になると b+1 段目の中立谺たちが「攻方の」歩の利きを持つので、これらの手はどれも今着手した受方のロイヤル駒への王手を生じさせる手となり不適切です。
このように、上記『 』の配置は手順「 (a,b)城、(1,b)→(a,b)△+ 」と整合性がありますが、ここでもし攻方の持駒に中立谺が存在したとすると、攻方は2手目の逆王手を(N-2,b)中立谺と打つことで回避できます(上記の通り 4 ≦ a ≦ L+1 であり、 L ≦ N-4 なので a ≦ N-3 です)。
よって、上記の長方形の領域にあるマスの数よりも迷彩中立谺の数の方が多いとすると、上記の手順と整合性があるが攻方が詰まないような配置の可能性が存在することになり、この手順で攻方が詰むと確定できないため、この手順は逃れとなります。
なお、上記『 』の状況で、上記の長方形の領域(これは横 a-3 筋、縦 N-1-b 段、計 (a-3) × (N-1-b) マスからなる)で n 枚の迷彩中立谺が使い切られていて攻方持駒に中立谺が存在しないとすると、上記の通り手順「 (a,b)城、(1,b)→(a,b)△+ 」は合法手であり、しかも2手目の逆王手を攻方が回避する手段がないため、この手順は詰みとなります。
以上の考察により、以下の事実が示されました。
事実3の条件 4 ≦ a ≦ L+1 、 3 ≦ b ≦ N-4 および (a-3) × (N-1-b) = n をすべて満たす(a,b)の可能性を考えます。
p = a-3 、 q = N-1-b とおくと 1 ≦ p ≦ L-2 、 3 ≦ q ≦ N-4 であり、 n = p × q が成り立ちます。
ここで p = 1 とすると n = q ですが、上の通り q ≦ N-4 である一方でパラメータの選び方から n ≧ N-3 であり、これらは矛盾します。
よって p = 1 とはならず、 2 ≦ p ≦ L-2 です。
上記の通り 2 ≦ p ≦ L-2 、 3 ≦ q ≦ N-4 かつ n = p × q ですが、パラメータの条件(#)により、これらを満たす p と q の組はちょうど1組だけ存在します。
そして、この唯一の(p,q)について、 a = p+3 、 b = N-1-q と定めると、この(a,b)は確かに事実3の条件を満たします。
よって以下が示されました。
以降では、「 (a,b)城、(1,b)→(a,b)△+ 」以外の手順はすべて逃れとなることを確認します。
まず、初手「 -X 」は2手目が何であっても逃れることを確かめます。
初手「 -X 」と整合性のある配置と手順の可能性として、 k = 3 と k = 4 の各々について
『初形で(1,k)△+が城+、(N-2,k)に中立谺があり、攻方の持駒に中立谺があり、初手(3,k)中立谺打』という可能性が存在します。 そのため、「 -X 」と指した時点では、迷彩中立谺の位置や覆面駒の種類は何も特定できません。
一方、初手「 -X 」で王手を掛けている駒は中立谺しかあり得ず、さらにこの中立谺は包か城の利きを1筋の△+のどれかから(直接または、他の中立谺を経由して間接的に)与えられている必要があります。
ここで、大元の△+が包+であるとすると、この包+から直接利きを与えられている中立谺が存在しますが、一方で事実1の帰結2.より、初形でこの包+と同じ段に中立谺は存在しません。
すると考えられる可能性は、初手でこの包+と同じ段に中立谺での着手をした場合のみですが、この場合にはこの包+および中立谺と同じ段に別の中立谺が存在しないことになり、初手で着手した中立谺が包+の利きを得ることで同じ段の N 筋にある攻方零+への利きが生じてしまいます。
つまり、初手が攻方自身への王手を生じさせる手となってしまい不適切です。
このことから、大元の△+は城+であり、この城+から直接利きを与えられている中立谺が存在します。 この中立谺の場所は3筋に限られるため、この中立谺が得ている城の利きにより大元の城+に王手が掛かります。 よって、2手目は少なくともこの王手を防げる手でなければなりません。 特に、合駒をする隙間が無いため、受方は駒を打ってこの王手を回避することはできません。
以上を踏まえますと、初手が「 -X 」の場合、2手目までの手順の可能性は以下のいずれかに限られます。 (上述した王手駒である中立谺と王手を掛けられている城+があるのは3段目から N-4 段目のいずれかであることに注意してください。)
前者の手順「 -X、-X 」について、考え得る可能性として、
『初形で(1,3)△+が城+、(N-2,3)、(3,2)が迷彩中立谺で、攻方の持駒に中立谺があり、初手(3,3)中立谺打、2手目(3,3)→(3,1)中立谺』および
『初形で(1,4)△+が城+、(N-2,4)、(3,5)が迷彩中立谺で、攻方の持駒に中立谺があり、初手(3,4)中立谺打、2手目(3,4)→(3,6)中立谺』はどちらも整合性があります。 そのため、2手目を指した時点で迷彩中立谺の位置や△+の種類は何も特定できません。 そして、これらの可能性『 』において2手目は逆王手ではないため、2手目で攻方が詰んでいることを受方は証明できません。 よって手順「 -X、-X 」は逃れとなります。
後者の手順「 -X、(1,k)→(3,k)△+ 」( 3 ≦ k ≦ N - 4 )について、上の考察より、考え得る可能性は
「初手を指した時点で(3,k)にある中立谺が(1,k)の△+=城+に王手を掛けており、2手目で(1,k)城+が(3,k)中立谺を取った」という場合に限られます。 この手順と整合性のある配置の可能性として、
『初形で(1,k)が城+、(N-2,k)が迷彩中立谺で、攻方の持駒に中立谺があり、初手(3,k)中立谺打、2手目(1,k)→(3,k)同城+』という可能性が存在します。 (この手順中、2手目に駒を取らない応手は不可能なので、(3,k)同城+は禁欲ルールに反しません。) そして、この可能性『 』において2手目は逆王手ではないため、2手目で攻方が詰んでいることを受方は証明できません。 よってこの手順「 -X、(1,k)→(3,k)△+ 」は逃れとなります。
以上のように、上記の2手目の可能性についてはいずれも逃れとなるので、以下の事実が成り立つことが確かめられました。
まず、以下の事実を注意しておきます。
「城の利きを持つある駒A(城自体か、城の利きを与えられた中立谺)が別の駒Bを跳び越えてその直後の中立谺Cへ取りを掛けている(そのことでCに城の利きが伝わっている)状態において、AとBの間の地点へ包+が移動することでAからCへ利きが伝わるのを防いだ」という場合に限られる。
これらの手順のうち、まず手順1「 (a,b)城、-X 」については、 a = 3 とするとこのような2手目で王手を回避することは不可能なので a ≧ 4 が成り立ち、条件を満たす配置の一つとして
『初形で盤面に中立谺は無く、受方の持駒に中立谺があり、初手(a,b)城、2手目(3,b)中立谺打』が得られます。
『初形で1筋の b-2 段目から b 段目までにある△+はすべて零+、(a,b-1)、(a,b-2)、(N-2,b-2)が迷彩中立谺で、初手(a,b)城、2手目(a,b-2)→(a,b)同中立谺』(初手を指した後の時点で、(a,b)城と、城の利きを持った(a,b-2)中立谺による両王手が掛かっています。 城からこれらの中立谺への利きを受方が遮断する隙間はありませんし、受方の手番においては中立歩から利きを伝えられている中立谺は存在しません(ので中立谺を歩の利きで動かすこともできません)ので、2手目に駒を取らない応手は存在しません。 よって2手目は禁欲ルールに反しません。 なお、(a,b-2)の中立谺から N 筋の攻方零+への利きは(N-2,b-2)の中立谺により遮られています。)
『初形で1筋の b 段目から b+2 段目までにある△+はすべて零+、(a,b+1)、(a,b+2)、(N-2,b+2)が迷彩中立谺で、初手(a,b)城、2手目(a,b+2)→(a,b)同中立谺』(上の場合と同様ですが、 N の選び方から b+2 ≦ N-3 であることに注意してください。)
『初形で1筋の b-2 段目から b 段目までにある△+はすべて零+、(a-1,b)、(a-2,b)、(a-2,b-1)、(a-2,b-2)、(N-2,b-2)が迷彩中立谺で、初手(a,b)城、2手目(a,b-2)→(a,b)同中立谺』(初手を指した後の時点で、城の利きを持った(a-2,b)および(a-2,b-2)の中立谺による両王手が掛かっており、城からこれらの中立谺への利きを遮断する隙間はありませんので、初手に対しては駒を取らない応手は存在しません。 なお、 N と a の選び方から a-2 ≧ 3 であることに注意してください。)
『初形で1筋の b 段目から b+2 段目までにある△+はすべて零+、(a-1,b)、(a-2,b)、(a-2,b+1)、(a-2,b+2)、(N-2,b+2)が迷彩中立谺で、初手(a,b)城、2手目(a,b + 2)→(a,b)同中立谺』(上の場合と同様ですが、 N の選び方から b+2 ≦ N-3 であることに注意してください。)
『初形で盤面に迷彩中立谺が存在しない』という配置が条件を満たしています。
以上により、手順1、手順2、手順5が逃れとなることが確かめられましたので、以下では残る手順3と手順4について考えます。
手順3「 (a,b)城、(c,d)零+ 」について考えます。
(a,b)と(c,d)は違う地点であることを注意しておきます。
また、盤面の条件より 3 ≦ b ≦ N-4 、 3 ≦ d ≦ N-4 です。
まず、 a = 3 のときは、初手が(a,b)城から(1,b)△+へ直接王手を掛ける手であり、合駒する隙間がありませんので、このような2手目の応手は不可能です。
よって a = 3 ではないので、以下では 4 ≦ a ≦ N-2 、 3 ≦ b ≦ N-4 、かつ 3 ≦ d ≦ N-4 の場合を考えます。
『初形で1筋にある△+はすべて零+、(3,b)、(a,2)、(a,1)、(N-3,1)、(N-2,1)、(N-2,N-4)、(N-2,N-3)が迷彩中立谺』(下図1は N = 11 の場合の一例)
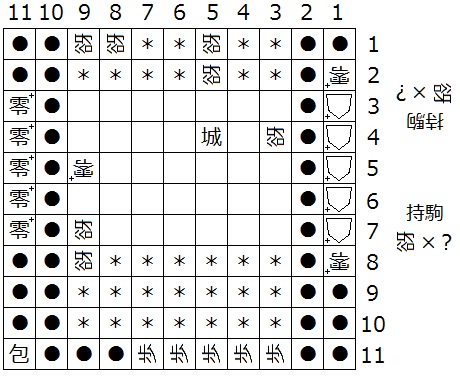
『初形で1筋にある△+はすべて零+、(a-1,b)、(a-2,b)、(3,b)、(a-2,2)、(a-2,1)、(N-3,1)、(N-2,1)、(N-2,N-4)、(N-2,N-3)が迷彩中立谺』(下図2は N = 11 の場合の一例)
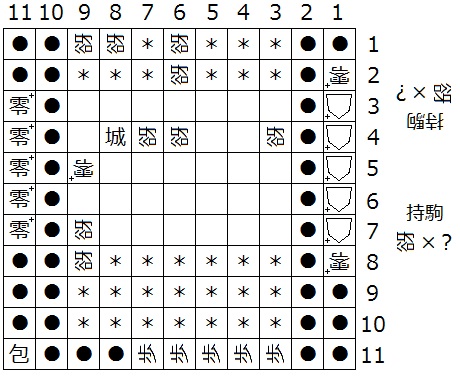
『初形で1筋にある△+はすべて零+、(3,b)、(N-2,N-4)、(N-2,N-3)が迷彩中立谺』(下図3は N = 11 の場合の一例)
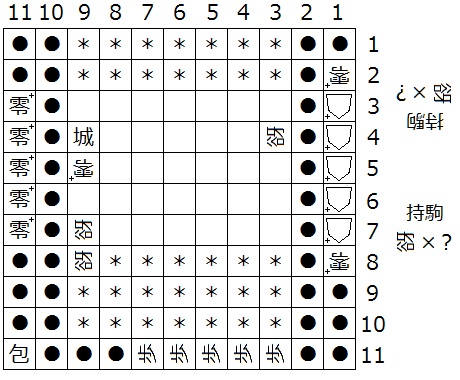
『初形で1筋にある△+はすべて零+、(3,b)、(N-2,2)、(N-2,1)、(N-3,1)、(N-4,1)、(N-4,N-4)、(N-4,N-3)、(3,2)が迷彩中立谺』(下図4は N = 11 の場合の一例)
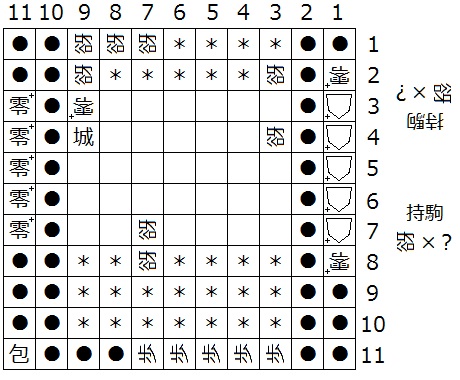
『初形で1筋にある△+はすべて零+、(3,b)、(a,2)、(a,1)、(N-4,1)、(N-3,1)、(N-3,d-1)、(N-3,d)、(N-2,d)、(3,2)が迷彩中立谺』(下図5は N = 11 の場合の一例)
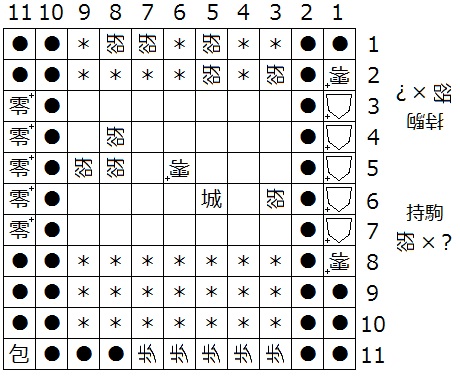
『初形で1筋にある△+はすべて零+、(5,b)、(4,b)、(3,b)、(4,2)、(4,1)、(N-4,1)、(N-3,1)、(N-3,d-1)、(N-3,d)、(N-2,d)、(3,2)が迷彩中立谺』(下図6は N = 11 の場合の一例)
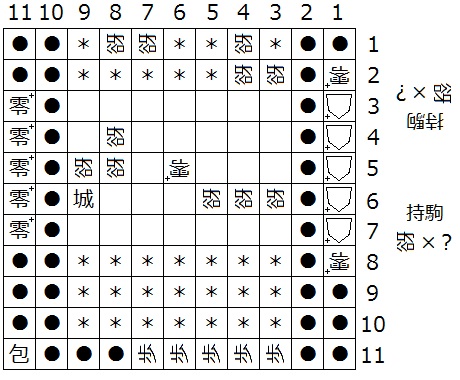
『初形で1筋にある△+はすべて零+、(5,b)、(4,b)、(3,b)、(4,N-3)、(4,N-2)、(N-4,N-2)、(N-3,N-2)、(N-3,d+1)、(N-3,d)、(N-2,d)、(3,2)が迷彩中立谺』(下図7は N = 11 の場合の一例)
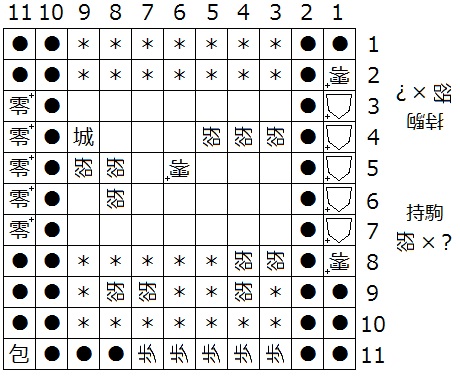
『初形で1筋にある△+はすべて零+、(3,b)、(a,d+1)、(a,d)、(N-2,d)が迷彩中立谺』(下図8は N = 11 の場合の一例)
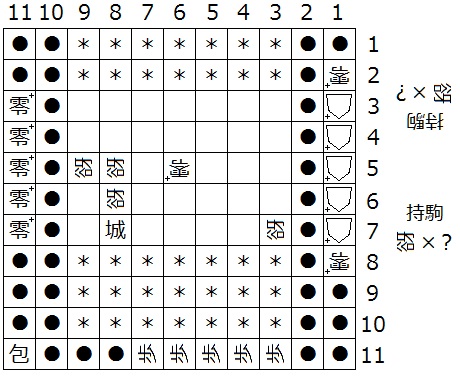
『初形で1筋にある△+はすべて零+、(3,b)、(a,d-1)、(a,d)、(N-2,d)が迷彩中立谺』(下図9は N = 11 の場合の一例)
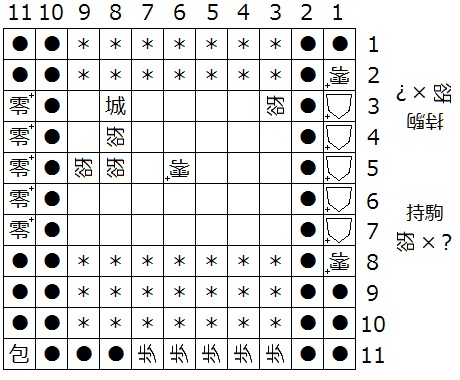
『初形で1筋にある△+はすべて零+、(5,b)、(4,b)、(3,b)、(4,N-3)、(4,N-2)、(N-4,N-2)、(a,N-2)、(a,d)、(N-2,d)が迷彩中立谺』(下図10は N = 11 の場合の一例)
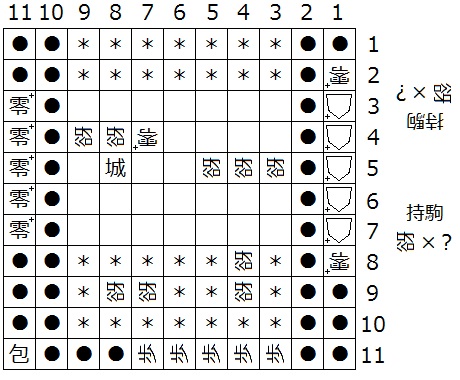
『初形で1筋にある△+はすべて零+、(5,b)、(4,b)、(3,b)、(4,2)、(4,1)、(N-4,1)、(a,1)、(a,d)、(N-2,d)が迷彩中立谺』(下図11は N = 11 の場合の一例)
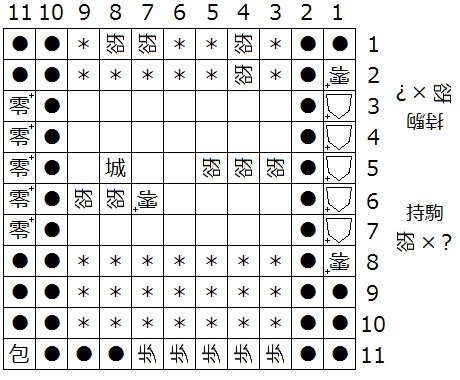
『盤面に迷彩中立谺は存在しない』
『初形で1筋にある△+はすべて零+、(3,b)、(N-4,b)、(N-3,b)、(N-2,b)、(N-3,2)、(N-3,1)、(4,1)、(3,1)、(3,2)、(3,3)、(N-2,3)が迷彩中立谺』(下図12は N = 11 の場合の一例)
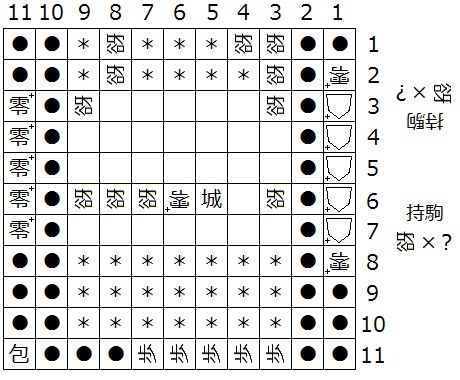
『初形で1筋にある△+はすべて零+、(3,b)、(a,N-3)、(a,N-2)、(N-5,N-2)、(N-4,N-2)、(N-4,2)、(N-4,1)、(4,1)、(3,1)、(3,2)、(3,3)、(N-2,3)が迷彩中立谺』(下図13は N = 11 の場合の一例)
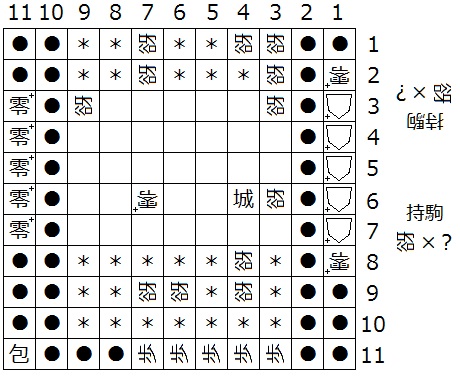
『初形で1筋にある△+はすべて零+、(a-1,b)、(a-2,b)、(3,b)、(a-2,N-3)、(a-2,N-2)、(N-5,N-2)、(N-4,N-2)、(N-4,2)、(N-4,1)、(4,1)、(3,1)、(3,2)、(3,3)、(N-2,3)が迷彩中立谺』(下図14は N = 11 の場合の一例)
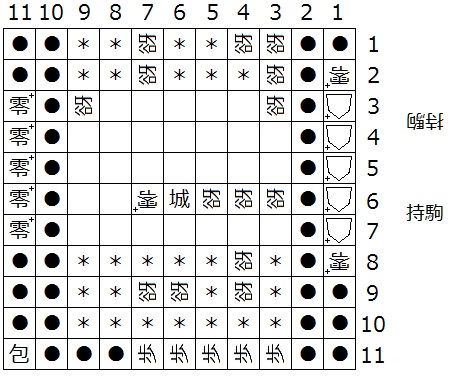
『初形で1筋にある△+はすべて零+、(3,b)、(a,N-2)、(a,N-1)、(N-3,N-2)、(N-2,N-2)、(N-2,d+1)、(N-2,d)、(3,d+1)が迷彩中立谺』(下図15は N = 11 の場合の一例)
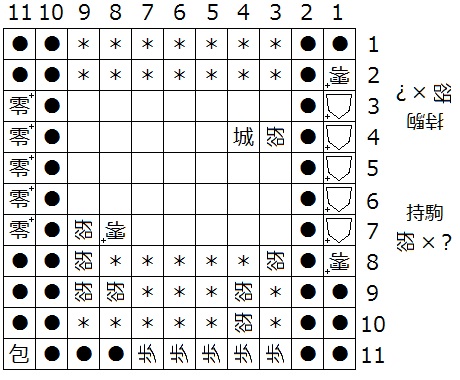
『初形で1筋にある△+はすべて零+、(5,b)、(4,b)、(3,b)、(4,N-2)、(4,N-1)、(N-3,N-2)、(N-2,N-2)、(N-2,d+1)、(N-2,d)、(3,d+1)が迷彩中立谺』(下図16は N = 11 の場合の一例)
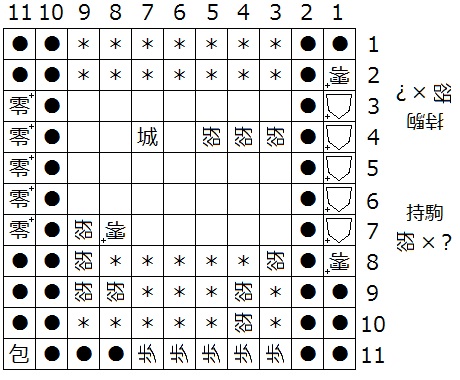
『初形で1筋にある△+はすべて零+、(3,b)、(a,2)、(a,1)、(4,1)、(3,1)、(3,2)、(3,3)、(N-2,3)が迷彩中立谺』(下図17は N = 11 の場合の一例)
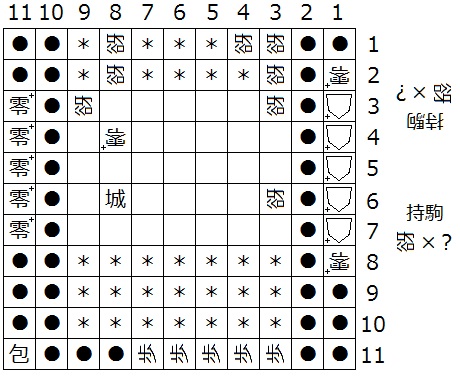
『初形で1筋にある△+はすべて零+、(3,b)、(a,N-3)、(a,N-2)、(4,N-2)、(3,N-2)、(3,N-3)、(3,N-4)、(N-2,N-4)が迷彩中立谺』(下図18は N = 11 の場合の一例)
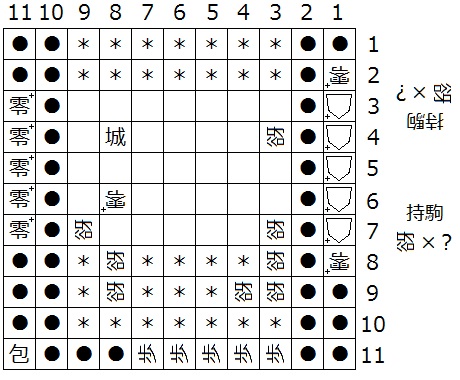
『初形で1筋にある△+はすべて零+、(5,b)、(4,b)、(3,b)、(4,2)、(4,1)、(N-4,1)、(N-3,1)、(N-3,N-2)、(N-3,N-1)、(4,N-1)、(3,N-1)、(3,N-2)、(3,N-3)が迷彩中立谺』(下図19は N = 11 の場合の一例)
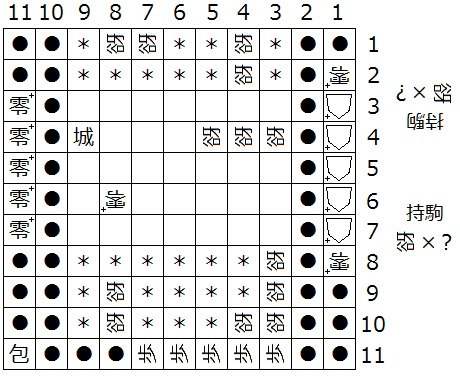
『初形で1筋にある△+はすべて零+、(3,b)、(a,2)、(a,1)、(N-4,1)、(N-3,1)、(N-3,N-2)、(N-3,N-1)、(4,N-1)、(3,N-1)、(3,N-2)、(3,N-3)が迷彩中立谺』(下図20は N = 11 の場合の一例)
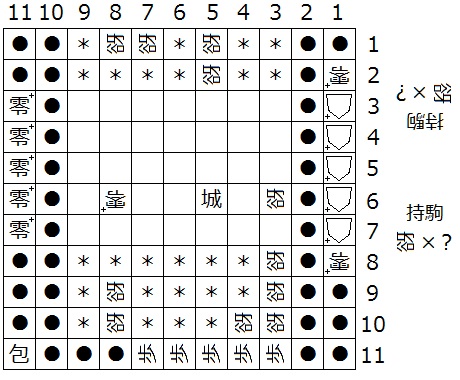
『初形で1筋にある△+はすべて零+、(5,b)、(4,b)、(3,b)、(4,2)、(4,1)、(N-4,1)、(N-3,1)、(N-3,N-2)、(N-3,N-1)、(4,N-1)、(3,N-1)、(3,N-2)、(3,N-3)が迷彩中立谺』(下図21は N = 11 の場合の一例)
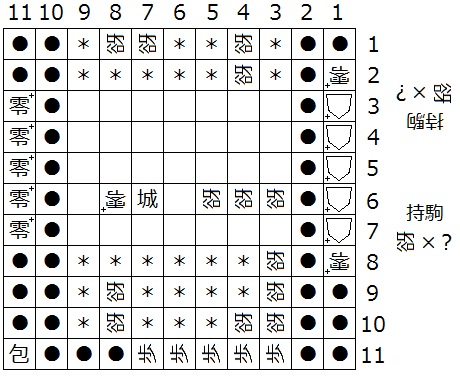
『初形で盤面に迷彩中立谺が存在しない』
手順4「 (a,b)城、(1,m)→(3,m)△+ 」( m ≠ b )について考えます。 盤面の条件より 3 ≦ b ≦ N-4 かつ 3 ≦ m ≦ N-4 です。
a = 3 とすると、初手で(3,b)の城が(1,b)△+に直接王手を掛けており、その王手は (1,m)→(3,m)△+ では回避できません。 よって a = 3 の可能性は無く、 4 ≦ a ≦ N-2 です。
a ≧ 5 のときは、条件を満たす配置の一つは、
『初形で1筋の m 段目以外の△+はすべて零+、(1,m)△+は城+であり、(4,b)、(a,2)、(a,1)、(4,1)、(3,1)、(3,N-2)、(3,N-1)、(N-3,N-2)、(N-2,N-2)、(N-2,N-3)が迷彩中立谺』(下図22は N = 11 の場合の一例)
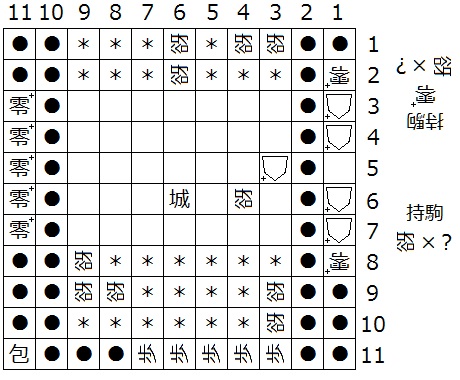
a = 4 のときは、条件を満たす配置の一つは、
『初形で1筋の m 段目以外の△+はすべて零+、(1,m)△+は城+であり、(3,b)、(4,2)、(4,1)、(5,1)、(6,1)、(6,m-1)、(6,m)、(N-2,m)が迷彩中立谺』(下図23は N = 11 の場合の一例)
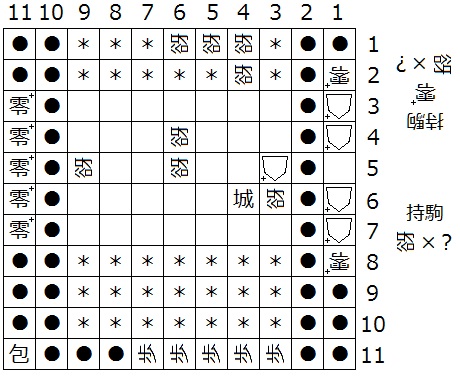
こうして、初手「 (a,b)城 」に対して、2手目「 (1,b)→(a,b)△+ 」以外の手はすべて逃れとなることが示されました。
以上より、冒頭の作意手順が本作における唯一の詰手順です。
【本作が完全作であることの証明終わり】
(c) Koji NUIDA 2018- All Rights Reserved.