The figures based on (2,2,p) are Prisms or Antiprisms.
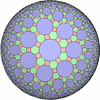
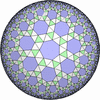
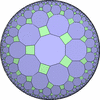
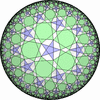
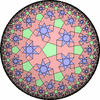
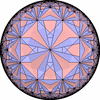
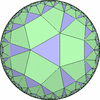
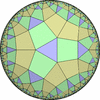
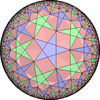
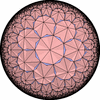
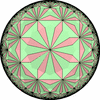
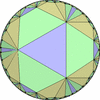
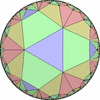
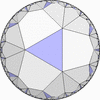
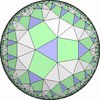
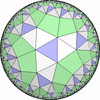
The figures based on (2,3,3), (2,3,4) or (2,3,5) are Uniform Polyhedra. The figures based on (2,3,6) are Uniform Tessellations on the Euclid plane. The figures based on (2,3,p>=7) are Uniform Tessellations on the Hyperbolic plane.
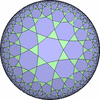
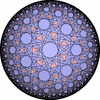
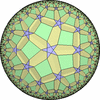
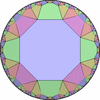
The figures based on (2,4,4) are Uniform tessellations on the Euclid plane. The others are Uniform Tessellations on the Hyperbolic plane.
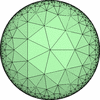
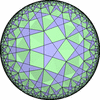
The figures based on (3,3,3) are Uniform tessellations on the Euclid plane. The others are Uniform Tessellations on the Hyperbolic plane.
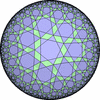
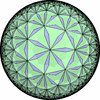
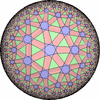
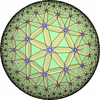
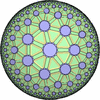
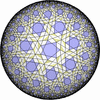
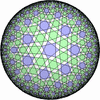
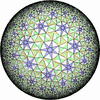
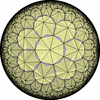
![[New]](new.png) I discovered new 13 uniform tessellations on the Euclid plane
(more detail).
I discovered new 13 uniform tessellations on the Euclid plane
(more detail).























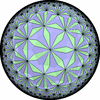


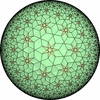



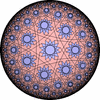

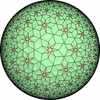
















![[update]](update.png)
![[3,3,3,4/3,4/3]](complex/s-22+2-2r_s.png)
![[3/2,Inf,3/2,Inf,3/2,4,4]](complex/sisrint_s.png)
![[3/2,Inf,3/2,Inf,3/2,4/3,4/3]](complex/gisrint_s.png)
![[3/2,Inf,3/2,Inf,3/2,12/5,6,12/5]](complex/sisstdobhint_s.png)
![[3/2,Inf,3/2,Inf,3/2,12/7,6/5,12/7]](complex/gisstdobhint_s.png)
![[3/2,Inf,3/2,Inf,3/2,12,6/5,12]](complex/sisdochint_s.png)
![[3/2,Inf,3/2,Inf,3/2,12/11,6,12/11]](complex/gisdochint_s.png)
![[3/2,Inf,3/2,4/3,4/3,3/2,4/3,4/3]](complex/sisdirint_s.png)
![[3/2,Inf,3/2,4/3,4/3,3/2,4,4]](complex/gisdirint_s.png)
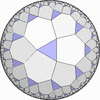

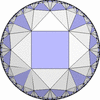
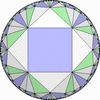
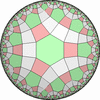

![[3/2,Inf,3/2,4,4,3/2,4/3,4/3]](complex/irsint_s.png)
![[4,Inf,4/3,8/3,4,8/3]](complex/irstobsint_s.png)
![[4,Inf,4/3,8,4/3,8]](complex/irocsint_s.png)
![[4,Inf,4/3,8/3,8]](complex/sirostobint_s.png)
![[4,Inf,4/3,8,8/3]](complex/girostobint_s.png)