初級問題 その1の答
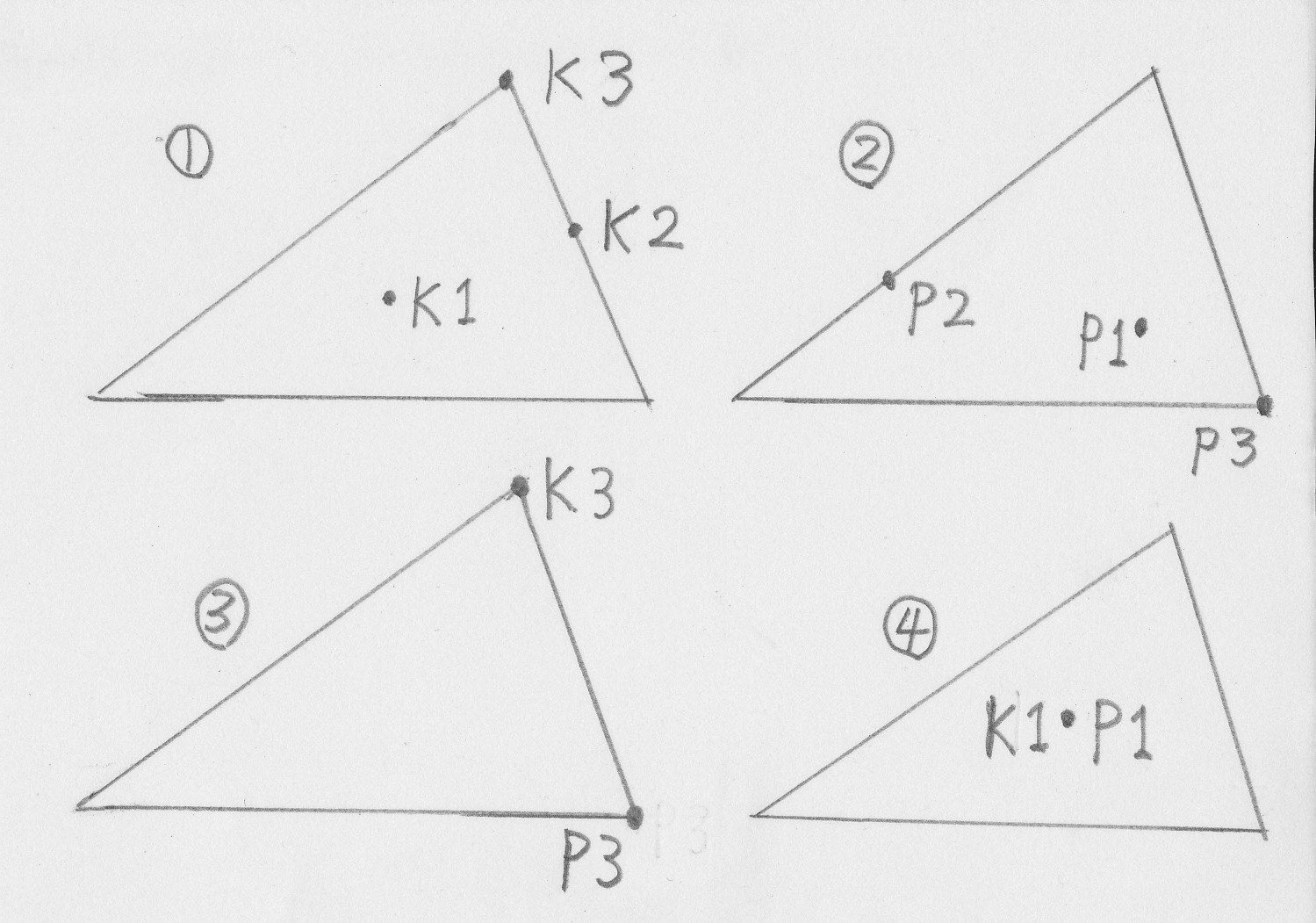
① 警備員は、K1ような三角形の内側(辺や頂点ではない、その内側の部分)、K2のような辺の上、K3のような頂点の、どこにでも配置することができる。
② 警備員は、どこに配置されていても、P1のような三角形の内側の一点、P2のような辺上の一点、P3のような頂点のどこにある一点も見ることができる。
③ K3にいる警備員が P3のような他の頂点を見ることもできる。これは幾何学の問題で、壁の厚さや柱の太さや警備員の体の大きさなどは一切考えないからである。
④ 警備員は、自分自身が立っている一点も、見ることができる。これはこの問題を解くこととは関係ないが、書かないと「盲点」ができそうなので、一応書いておこう。
上の①②③④の事柄を公理のように考えるからこそ、3角形の部屋は1人の警備員で見ることができると言えるのである。よって、上の①〜④を公理①〜④と呼ぶことにしよう。
初級問題 その2
4角形の部屋はなぜ1人の警備員で見渡すことができるのか。
初級問題 その2の答
① 凸角だけの四角形。
Kが四角形の内側にある時は、Kを頂点として共有する四つの三角形に分けることができる。Kが辺の上にあるときは、Kを頂点として共有する3つの三角形に分けることができる。Kが頂点の上にあるときは、Kを頂点として共有する二つの三角形に分けることができる。よって、①②の公理によって、警備員はどこにいても、四角形の内部をすべて見ることができる。

そこで、今度は上記の中で上級問題を解くために必要な命題を定理として記録しておこう。
定理① 凸角だけの四角形は、どの頂点からも全体を見渡すことができる。
② 凹角を含む四角形。
その凹角に隣接する頂点aとその凹角を直線で結んでaと反対の方向に伸ばせば、三角形Aを作ることができる。このAの中にいる警備員は、①②の公理によって、A全体を見ることができる。また、bとその凹角を直線で結んでbと反対の方向に伸ばせば、三角形Bを作ることができる。このBの中にいる警備員は、①②の公理によって、B全体を見ることができる。したがって、ABの重なった部分にいる警備員は四角形全体を見ることができる。
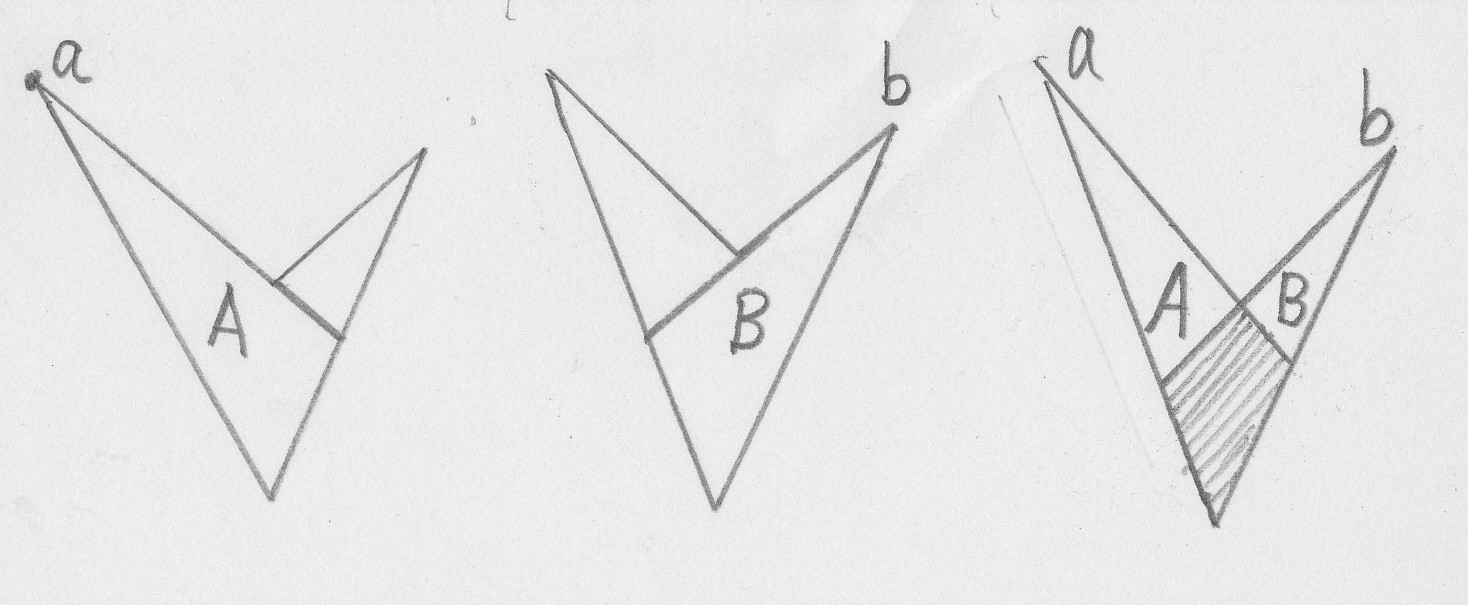
定理② 凹角を含む四角形は、凹角の頂点とその対角の頂点からは全体を見渡すことができ、凹角の頂点に隣接する頂点からは全体を見渡すことができない。
初級問題 その3
5角形の部屋はなぜ1人の警備員で見渡すことができるのか。
初級問題 その3の答
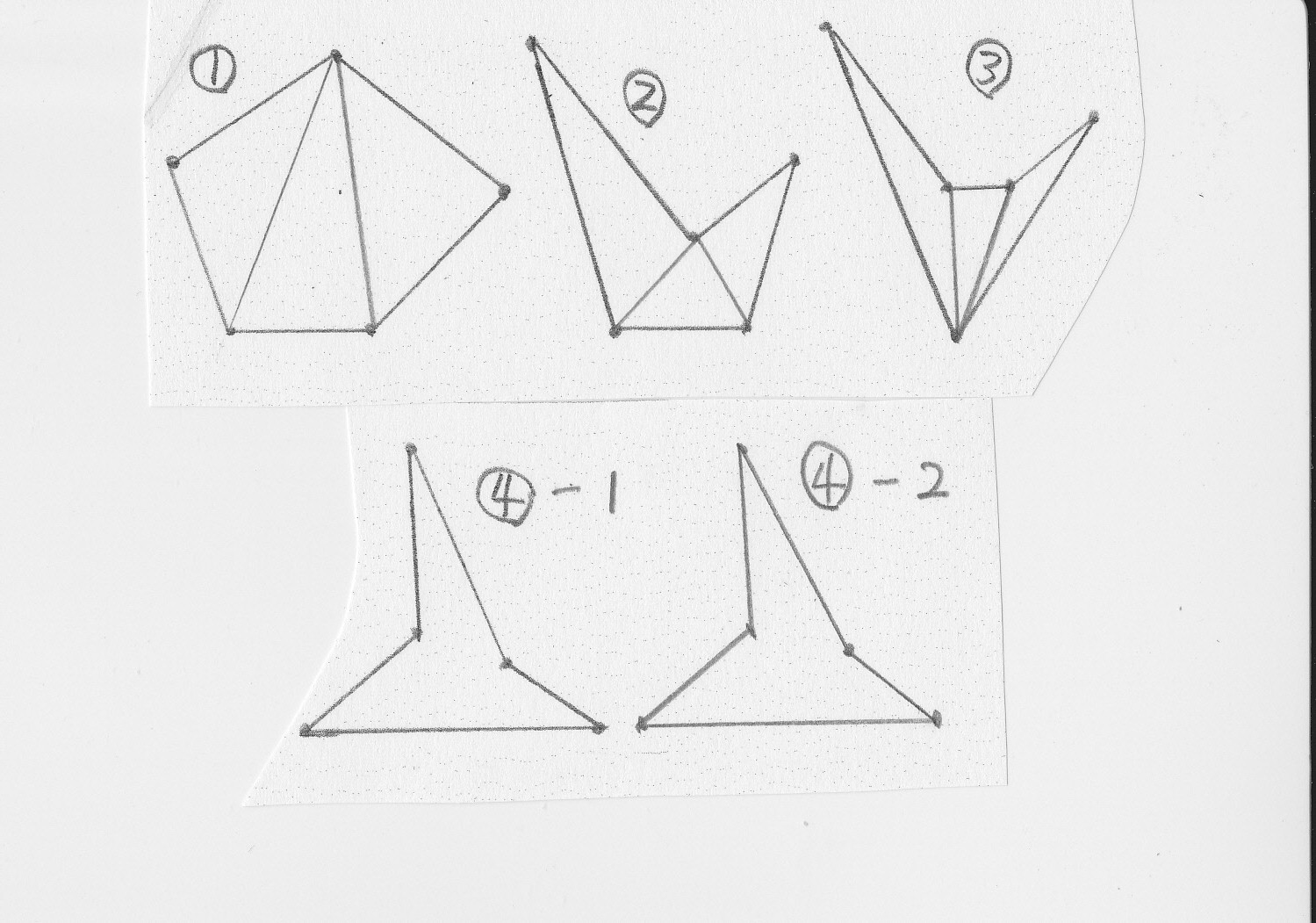
説明をある程度省略しながら結論を急ぐと、
定理③ 凸角だけからできている五角形は、どの頂点からも全体を見渡すことができる。
定理④ 一つの凹角を含む五角形は、その凹角の頂点から全体を見渡すことができ、凹角の頂点に隣接する頂点からは全体を見渡すことができない。
定理⑤ 隣り合った凹角の頂点を持つ五角形は、その隣り合った凹角の頂点と向き合う位置の頂点から全体を見ることができる。
定理⑥ 隣り合わない二つの凹角の頂点を持つ五角形は、小さい凹角の頂点からは全体を見渡すことができる。(証明は後回し)
初級問題 その4の答(後回し)
中級問題に移る 上級問題に移る
j