凹凸の角の入り混じったn角形の展示室があるとする。警備員をこの展示室の所定の位置に配置する。もちろん展示室は平面図形としての多角形の比喩であり、警備員は点の比喩である。警備員は周囲を見渡すが、歩くことは出来ない。n=3またはn=4であれば、明らかに1人で十分だが、下図に示すようにn=5でも1人で十分である。しかし、n=6では、1人で済む場合もあるが、たとえば下図のような形の展示室なら2人の警備員を必要とする。つまり、必要最小限の警備員の数は2である。点が警備員の位置である。
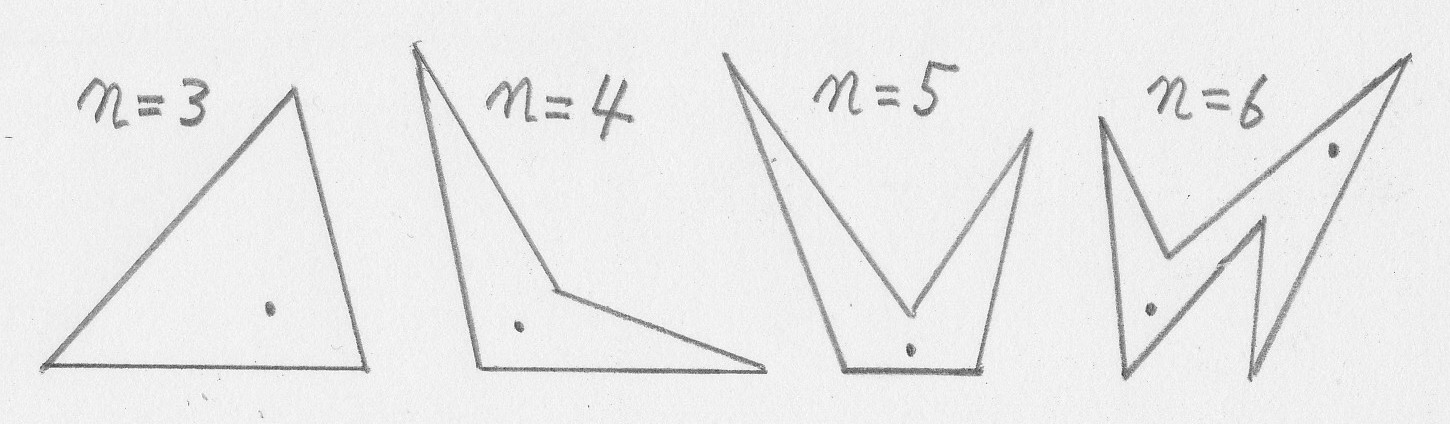
すべての壁面を見渡すのに必要最小限の警備員の人数をmとし、nの関数で表せ。
この問題は、もう少しで解けると思いながら、2011年8月1日から9月14日までの酒を飲んでいる時間のすべて、つまり90時間を費やしても解けなかった。数学の先生に聞いたら、これは数学者が論文を書いて証明するようなきわめて難しい問題で、とても私のような素人には解けない問題であるということだった(もちろん、そういう言い方はしなかったが)。
また、その解答を教えてもらったが、私の予想した解答とは違っていた。この問題を解いた論文は、インターネットで、『美術館監視問題』のキーワードで検索すれば、読むことができる。しかし、これはたぶん、高校数学の領域をはるかに超えた内容を含んでいるようだ。
しかし、失敗したとはいえ、知恵を絞って考えたり書いたりしたものを全部捨てるのは勿体ないので、初級問題や中級問題で意味がありそうなものは残しておくことにしよう。私は数学者の書いた論文を読もうとは思わない。また、読んでも分からない。しかし、今後も自分なりの方法で、この問題と付き合い続けようとおもう。例えば、9角形で、3人の監視員を必要とする多角形があるそうだが、それはどんな形で、どう考えれば描けるのか、などは中級問題になり得るかも知れない。その他。
初級問題に移る 中級問題に移る メニュー画面に戻る