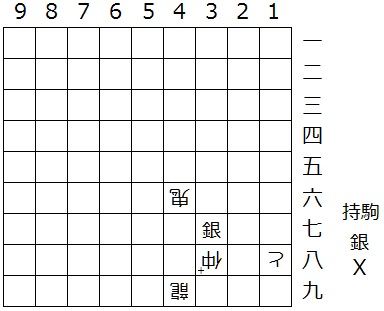
ルール：詰将棋（N×9盤、N≧8） ５手 （特殊ルールの説明）
＊「X」は覆面駒で、種類は「(m,0)-rider」（mは整数、m≧2）のいずれかとします。
＊＊「(m,0)-rider」は本作でだけ導入した駒で、左側一方向か右側一方向にmマスずつ跳ねて進める駒です（着地点に駒があるとそこから先へは進めません。着地点が相手の駒ならばそれを取れます）。
＊盤面の「鬼」の位置は([N/4]+2,6)、ここで[N/4]はN/4の整数部分を表わします。
（上図はN = 9の例、下図はN = 19の例）
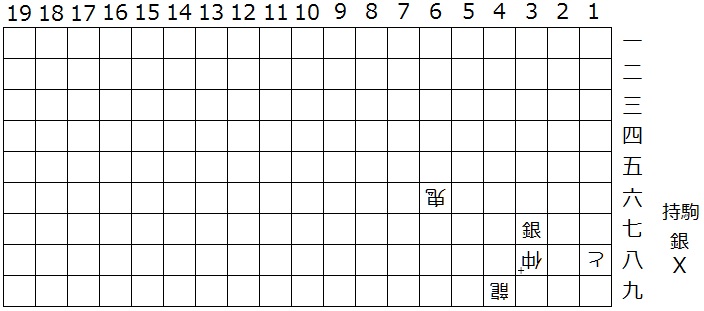
（「Web Fairy Paradise」107号掲載、2017年5月）
特殊ルール詰将棋を扱うインターネット配信誌「Web Fairy Paradise」で、大きさが可変な（変数を使って指定されている）盤面を使っている作品を目にして、こういう盤面を使ったら何か面白いことができないかなぁと思って考えた作品です。
（以下、ネタバレ回避のための改行）
.
.
.
.
.
.
.
.
.
"Bertrand's postulate"と呼ばれる整数論の定理があります。
これには同値な表現がいくつかありますが、最も良く知られている表現の一つは「nを1より大きな整数とすると、n < p < 2nを満たす素数pが存在する」というものです。
（"postulate"（仮説）という名前が付いていますが、きちんと証明された定理です。
"Bertrand-Chebyshev theorem"などと呼ばれることもあります。）
この作品は、「すべてのN≧8についてこの図が完全作である」こととBertrand's postulateが同値である、という性質を持つ作品です。
きちんと調べたわけではありませんが、まず間違いなく、こうした性質を持つ作品は世界初でしょう。
もう少し詳しく述べますと、作意手順自体にはBertrand's postulateは関係が無いのですが、とある変化手順が詰む（しかも作意よりも短く）かどうかにBertrand's postulateが関係してくる、という仕組みです。
このような性質を実現するために「(m,0)-riderに限定された覆面駒」という強引な手段を導入する羽目にはなりましたが、使用駒数を少なくできて、また手順にも一応捨駒が入ったことで最低限の格好は付いたかな、と思っています。
なお、こんなハチャメチャな作品でも、出題時にはちゃんと作者の狙いを看破した解答が寄せられました。
ありがたいものです。
Web Fairy Paradise誌で行われた年間発表作への投票「Fairy TopIX 2017」で本作が短編部門２位を受賞しました。 ご投票いただいた皆様どうもありがとうございます。
(c) Koji NUIDA 2017- All Rights Reserved.