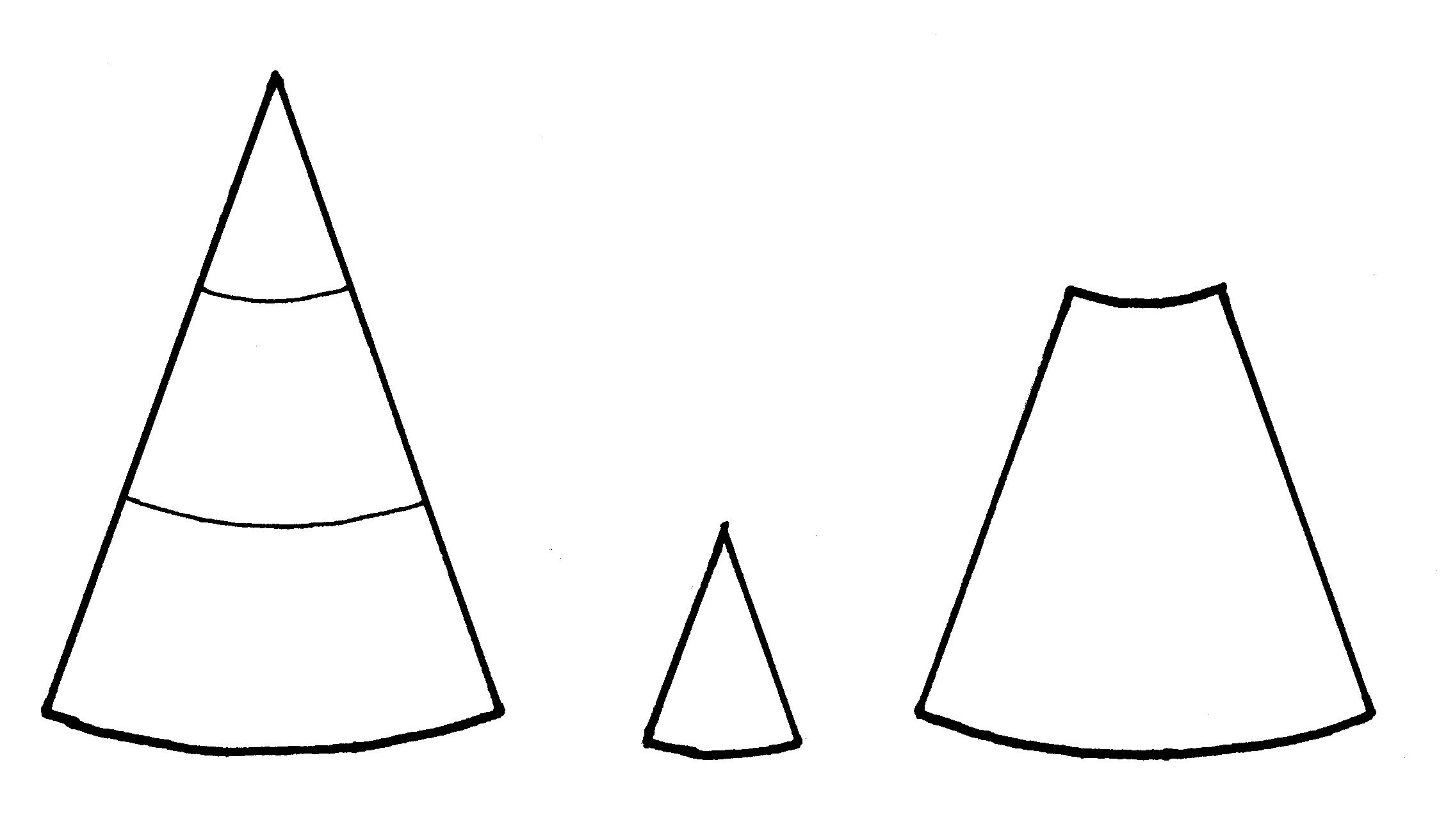
上の左の写真の扇形の面積が27なら、一番右の図形の面積は24です。しかし、見た目で答えると、20~24位の答が多いです。
この問題はもとになる円の直径や、扇形を切り取った中心角の大きさを変数で定義し、公式を用いて計算すれば、答は出ます。
しかし、実はもっと簡単な解き方がある。それは次の公式のようなものを使います。
①互いに相似である平面図形の面積は、相似比の二乗に比例する。
これを使うと、切り取った部分は3、残った部分は24と、暗算で答が出ます。しかし、大切な点は、計算せずに出した答が、実際より小さめだと言うことです。
上級問題 答
この問題も底面の直径や円錐の高さを変数で定義し、錘の体積の公式を用いて計算すると、一番右の立体の体積は26となります。
これも、もっと簡単な解き方があり、それは次の公式のようなものを使います。
②互いに相似である立体の体積は、相似比の三乗に比例する。
これを使うと、大きな円錐と小さな円錐の体積の比は27:1なので、残りの部分は26と暗算で出ます。
しかし、大切なのはそのことではない。この二つの図形を見せて、「見た感じで、右の立体の体積はどれくらいか」と質問すると、人は普通、どう感じるだろうか。東大、慶応、早稲田などの学生に実験的に聞いてみたところ、答は21~23が多かった。実際、誰が見ても、同じように感じるでしょう。となると、切り取った部分の体積の目測は、5倍も間違っていることになる。人間は、立体を理解したり測ったりするとき、平面に直して理解したり測る癖があるようだ。しかし、平面の場合でも、つまり、初級問題でも、切り取った部分の面積は3にしかならないのだが。
この問題が教える教訓は、人間の五感や第六感、あるいは感情的判断が、非常に不確かだということです。だから、数学や物理や論理的判断は、世界を正確に理解するための非常に頼りになる道具なのです。ケプラーもニュートンもアインシュタインも、数学を道具にして宇宙の現象を解明し、人々に説明しました。
昔の建物や構築物、たとえば五重の塔や京の五条の大橋などは、職人が経験で作ったが、どの程度の地震や強風に耐えられるかは、それが実際に起きるまでは分らなかったのです。現代の超高層ビルや橋、その他のあらゆる構築物は、数学を学んだ建築家が設計し、コンピュータに計算させて作ります。そして、出来上がった構造物が、どの程度の地震、どの程度の嵐に耐えられえるかということは、前もって計算することができるのです。
大地震が起きたとき、現代の建物は倒れたが、五重の塔は倒れなかったなどということがあったからといって、昔の技術が現代の技術より優れていたとは言えない。昔は、耐震性など計算できなかったから、むやみに地震に強い建物を作ったのです。現代の建物は、一定程度の地震には耐えられるように計算されて作られている。それを越える地震が起きたので建物が倒れた、とすれば、それはある意味で、科学の勝利なのです
上級問題に戻る。
メニュー画面に戻る。