市原市の算額

2015年4月8日、市原市不入斗（いりやまず；　有秋台の近く、内房線姉ヶ崎駅→バス有秋東小学校停留所）の薬王寺に行って、算額を見ました。

	年に一度、4/8のお花祭りの日に公開されます（算額が保管されているお堂の仏像の公開と合わせているとのことです）。今年は小雪が混じる雨の中、檀家の皆さんが客人のおもてなしをしていました。ご苦労様です。
	仏像の右に算額が置かれていました。 「　関流石富法門人　鈴木大介俊直　 　　　　寛政元年酉十月吉辰　」 書かれたのは1789年とあります。天災が続いた後、明治維新を向かえようとする時期にこの算額が書かれました。浮き彫りがなされ、この地の文化水準を誇らしげに示しているのかもしれません。
	現代になって亀子さんという方が算額の内容について解説書を作られています。この算額を大切にしている地の心があります。
	算額解説書の最初のページは拓本？江戸時代はコピーをとるのは容易ではありませんでした。この算額のように図/字が浮き彫りになっていると拓本を取って勉強をすることができます。
解説書第２頁には点を振った文章が書かれています。 市原市薬王寺算額　　亀子 今有如図鈎股弦之内容小円径与中円径及大円半径、只云者、鈎五百八十八寸、股二千令一十六寸、弦二千一百寸、問大中小各円径幾何。 　答曰、大円半径　三百四十三寸、 　　　　　中円径　　五百令四寸、 　　　　　小円径　　一百二十六寸、 術曰、列鈎、加入股、得数内減弦余得中円径数、折半之、名甲、列股、内減甲、余以鈎相乗之、名乙、自乗之、名丙、列弦以乙相乗之、倍之、名丁、列中円径、以鈎寡相乗名庚、列弦寡内減鈎寡、余名辛、以丙相乗之、得数以之減庚、余除平方、見商数以之減己余以辛除之、得商大円半径数、列甲自乗之、名子、列鈎、内減甲、余名丑、自乗之、名寅、列子加入寅、得数除乎方、見商数名卯、内減甲、余名辰、以甲相乗之、得数以丑除見商数、名己、列辰、以卯、相乗之得数以己除之、見商数名午列辰、以己相乗之、倍之、為実、列己、加入午、得数為法、除実、得商小円径数、合問。 　関流石富法門人　鈴木大介俊直　　　寛政元年酉十月吉辰
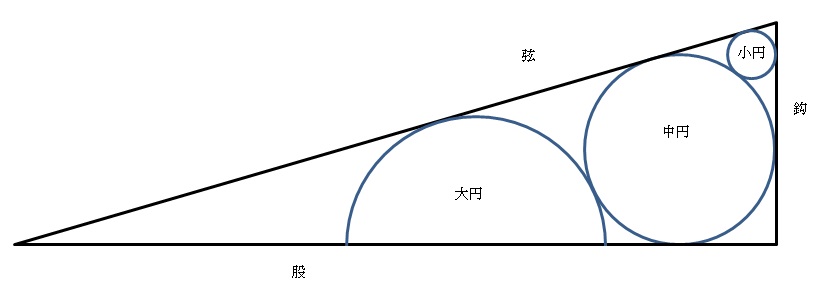
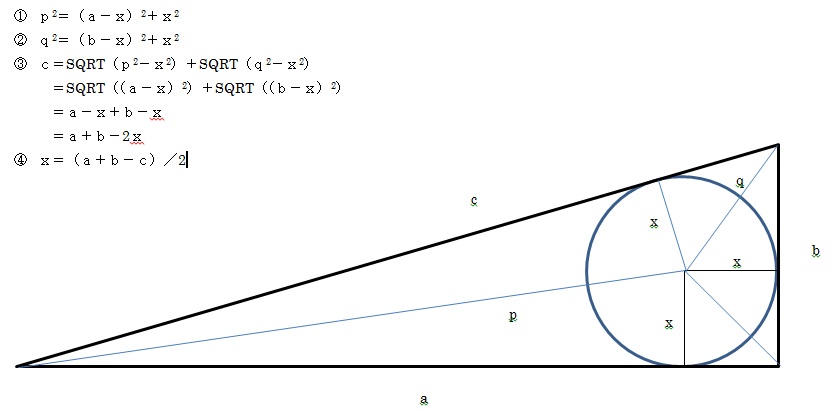
現代語訳 小輩的なこの算額の訳は次のような感じになります。 図のような小円と中円及び大円が内接する三角形がある。　但し、高さ588cm、底辺2016cm、斜辺2100cm。 問題：　大中小各円の径はいかに。 答え：　大円の半径は　343cm 　　　 　中円の直径は　504cm 　　　 　小円の直径は　126cm 1.中円の直径　（まず直角三角形に内接する中円の直径を求める） 高さに底辺を加算して斜辺を減算すれば中円の直径を得ることができる　（詳細は関流としては簡単なので原文では省略されていると思われる） 2.大円の半径 ・・・ 3.小円の直径 ・・・ 第３頁以降には、現代語訳、現代風解き方が書かれています。　その内容は亀子さんの著作権に触れるような範疇になるので亀子さんの解説書の内容はここには書きません。
小輩がこの問題を考えた範囲で解法を以下に書きます。現代の数学では下のように解くことができます（あくまで参考なもので、ベストアンサーではありません）。 解法は、始めに直角三角形に内接する中円の直径を求めて、その中円に接してかつこの三角形の残りの空間で内接する半円の半径を求め、また、中円に接してかつこの三角形の残りの空間で内接する小円の直径を求めるというものです。 現代のﾚﾍﾞﾙの高い中学生だったらできるものと思います。 まず中円。
大半円と小円については、一例として補助線を引くことによって、上の方程式で解くことができます。二次方程式を解くことになるので、その方程式を解くと答えは各々２つ出てきますが、問題に「図のような三角形」と書かれているので、その条件にあった値が答えになります。条件わけをして答える というのは高校レベル。高校／大学入試の数学を懐かしく思い出します。条件わけの仕方を身につけると高校の数学の壁を乗り越えることができます。
薬王寺を訪問した時に住職さん（4/8だけ薬王寺に来られる？）と話した時に、住職さんもこの問題を解いてみた という話を伺いました。この算額が現代にもいい影響を残している と感じました。 この算額に書かれたような数学が日本全国に広まったことによって、明治維新に西洋の文明が入ってきた時に基礎的な力があったからこそ文明を受け入れることができて各分野が発展したと考えています

小輩は和算／算額の専門家／マニアではないので、独特の解法／術は知りません、が、江戸時代の数学のレベルには関心があります。小輩にとって和算／算額は縄文時代の土器と同様に歴史の一要素です。

トップページに戻る