3. �_�C�}�[�̃��g
�@�@ �����ł͊ȗ��ȃ��f���Ƃ��āA���m�}�[�Ƀ��ʂɐ��f���t�����A���ʂɃ��W�J�������郉�W�J�����q���U�����ă_�C�}�[������������̂��l����B
�@�A�@ghemical���N������B�ŏ��Ƀ��m�}�[�̃t�@�C����open���A���ɓ�����ʂł��̃��m�}�[�̃��W�J�����q��open����B���W�J�����q�͓��F�ɕ\�������B�utransXY�v��I������<shift>�������Ȃ��烉�W�J�����q����۰����ƃ��W�J�����q�����ړ�����B�r�j�����C�G�e�B�ʂŌ�����悤�ɂ��ă��W�J�����q�̃��W�J�����q�����m�}�[���q�̃��ʌ��q���d�Ȃ�悤�Ƀ��W�J�����q���ړ������ĂP�A�̂����ŕ��q�̍��W�t�@�C�������B
�@�B �G�f�B�^�Ńt�@�C���̓��e���������Ƀ��W�J�����q�̍ŏ��̌��q�̌������u1 2 3�v�ɂȂ��ĂȂ��Ă��Ȃ����͍ēxghemical�ɖ߂��ĂP�@�̂����Ń��f�B�J�����q�̈ʒu���œK�Ȉʒu�ɂ��č��W�t�@�C������蒼���B
�@�C �G�f�B�^���N�����ĕ��q���W�t�@�C�����Ăяo���A�L�[���[�h���upm3 EF PRECISE DEBUG geo-ok�v�Ƃ��A���W�J�����q�̍ŏ��̌��q�̌��q�ԋ������u2.6�v�Ƃ��A�����e�k���u-1�v�Ƃ��A���̂y-matrix�̍ŏI�s�ɋs�Ɓu2.5 2.4 2.3 2.2 2.1 2.0 1.9�v�̍s�������ăt�@�C����ۑ�����B
�@�@�@�y-matrix�́@�Ⴆ�Ύ��̂悤�ɂȂ�B
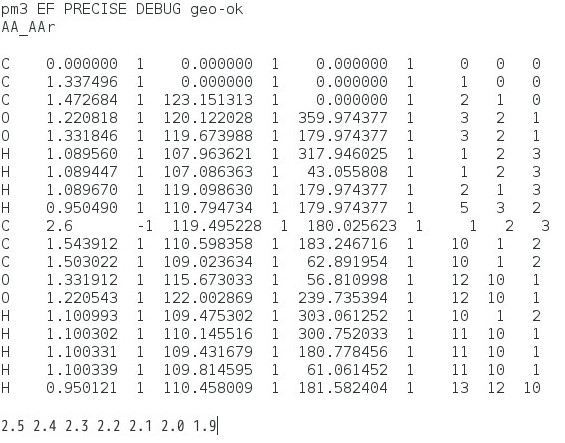
�@�D MOPAC���N�����ĂR�C�ō쐬�������e�̂y-matrix��FOR005�ɕۑ�������MOPAC�V�̌v�Z���s���AFOR012���Ăт����ă��g�̋ɑ�l�����߂�B
4. �������G�l���M�[
�@�@�@�R�œ���ꂽ�_�C�}�[�̃��g�̋ɑ�l����P�œ���ꂽ���m�}�[�̃��g�ƂQ�œ���ꂽ���W�J�����q�̃��g�����������Ċ������G�l���M�[���v�Z����B
�@�A �e���m�}�[�ɂ��ă_�C�}�[�������̊������G�l���M�[�����\�Ɏ����B
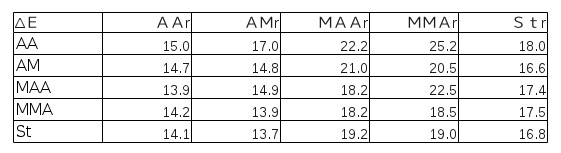
�T. �܂Ƃ�
�@�@�����œ���ꂽ���d�͗��z�I�d�������Ōv�Z���ꂽ�l�ł���A�܂��A���f�����O�ɂ��Ă������̉��肪����A�����܂ł��ڈ��̒l�B���ۂ̔����ł͗n��x�Ƃ��n�}���ʂȂǂ��傫�����ʂ��Ⴄ���̂ɂ���B�hpolymer handbook�h�ɂ͋��d���Ɋւ��鏔�X�������l��������Ă��邪�����n�}���ς��ƒl���傫���ς���Ă��邱�Ƃ�����A���ۂ̔����ƕ��q�O���@�̌v�Z�l���߂Â��邽�߂ɂ͔����n�}�̉e�����l�����Ȃ���Ȃ�Ȃ��B�@�Ƃ������ƂŁA�����ł͂���ȏ�Nj����Ȃ����A�������郂�m�}�[������i�Ⴆ�β��ݎ_�����ِe������ρA���ͷ�ٱ��َ_���a������ρj���l�Ȍv�Z�����Ă����Ōv�Z�������m�}�[�̒l�Ƒ�G�c�Ȕ�r�����邱�Ƃ͂�����x�Ӗ�������ƍl����B
�g�b�v�y�[�W�ɖ߂�