☆ 円に内接する正多角形
円に内接する正五角形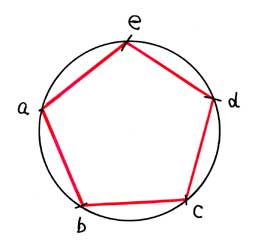 |
こちらも円に内接する正多角形として描きます。
皆さんご存知の正六角形と同じ方法です。
六角形の場合、円の半径で円弧を切っていくと円周に6個の交点が出来ます。
この交点を結べば正六角形が描けます。
このようにして描いた正六角形の一辺は円の半径と同じです。
一辺3センチの正六角形を描きたければ、
半径3センチの円を描けばよいのです。
では、一辺3センチの正五角形の場合どんな大きさの円をかけばよいのでしょうか。
これが分かれば簡単ですね。
☆ 求める計算式
比較的簡単な図形の問題です。
ここでは解説は省略しますが、次の式で求めることが出来ます。
R = m/2sin(180/n) n:多角形の辺(正n角形)の数
m:正多角形の辺の長さ
R:求める円の半径
☆ 表計算(Excel)を使って計算する
計算式で難しいのは三角関数の計算ですね。
三角関数で躓いて数学が嫌いになったんだぞ!、三角関係と共に解くのが難しい…
お怒りにならず続きを読んでください。
表計算(Excel)を使えば三角関数も簡単です。一辺3センチの正五角形を例に説明します。
① Excelを立ち上げ、セルA1に半角の数字3(辺の長さ)を入れてください。
② セルB1には =2*SIN(RADIANS(180/5)) をコピペ(コピー&ペースト)で入れます。
エンターキーを押した瞬間にセルB1には1.175570505と表示されます。
2sin(180/n)、nが5の場合、の数式が計算されたのです。
③ セルC1には =A1/B1 と入力します。…コピペでも可
エンターキーを押した瞬間にセルC1には2.551952425と表示されます。
これが求める解です。すなわち2.55センチの円を描けば良いと分かります。
☆ 求める値を表にしました
上記の計算式をエクセルの関数機能を使って計算すれば求めることが出来ます。
これも面倒と云われそうです。
手っ取り早く解を求めるために、辺の長さ3センチの正多角形を例に計算した結果を次の表にしました。
| 正多角形の種類 | 円の半径 |
| 3 | 1.73 |
| 4 | 2.12 |
| 5 | 2.55 |
| 6 | 3.00 |
| 7 | 3.46 |
| 8 | 3.92 |
| 9 | 4.39 |
| 10 | 4.85 |
辺が3センチの正五角形を描くには、半径2.55センチの円を描き、コンパスの幅3センチにして基点aから円弧を切り交点b、c、d、eを求めます。
次に赤い線のように交点を結ぶと正5角形が完成します。
表には正十角形まで載せていますので、各種の正多角形を描いてください。
☆ 大きさの異なる多角形を描くには比例計算
上の表は辺が3センチの正多角形を描く円の半径です。
4センチの多角形ならば4/3=1.333を掛ければ、円の半径を求められます。
|