

| レンズを使用する人にとって何よりも大切なことは、そのレンズがどのような目的に用い |
| られるか?と言う事と、その作る画像の品質とをよく知っていることです。 しかしレンズ |
| の所有者で、この他に更にレンズの構造やそれによって定まる収差補正の可能性など |
| についても興味を持つ人が次第に増加しています。 それで次に種々のライカ用レンズ |
| に対し、その構造を断面図により、又、特殊の収差補正方法を言いながらライカレンズの |
| 性能を説明したいと思います。ここではレンズの解像力について数字的に表示すること |
| は致しません。 解像力には種々なファクター、例えば撮影用感光材料の性質などが |
| 決低的な役割を持つており、しかもこれらのファクターを規格に普遍的に一定化されて |
| いないからです。 |
|
|
| エルマー f=5cm 1:3,5 |
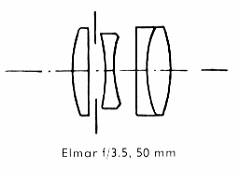 |
| このレンズの構造に関してはよく知られた変形トリプレットで三体のレンズ群よりなり、最後 |
| の群は集光性のバルサム面を持つており、これは良好な収差補正条件において比較的 |
| 簡単な構造を示す形式であります。このレンズではこの形式に許された収差補正の可能性 |
| は十二分に利用され、すべての残留収差は(単色収差も色収差も)互いに良くバランスして、 |
| ライカ判に適応した、特に良好な一般補正状態となっています。鮮鋭度は絞り全開でも |
| すべてにいちじるしく高いのですが、絞ると共に更に急速に向上し、絞りがおよそ8で最大値 |
| に達します。これはエルマーに限ったことではなく、ごく一般に通用することですが、一言付け |
| 加えておきます。焦点深度を増すためにレンズをいわゆる「臨界口径」(最適絞り)より更に |
| 絞り込むと、回折の現象によって解像力が減退する、と言うことは理論的には期待される |
| ところです。しかし解像力が1mmに約100本位までの通常の感光材料を用いる場合には、 |
| 実用的には絞り16において解像力の減退は普通全然認められません。もちろん特に高解 |
| 像力のフィルムを使って細かい試験用の白黒図形を撮影するような場合は、別に考えなけ |
| ればなりませんが。 |
| ズミター f=5cm 1:2
|
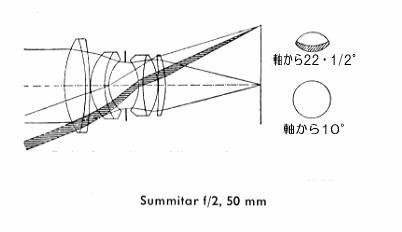 |
| エルマーより明るいレンズ、ズミターはいわゆるガウス型レンズを基礎としたもので、口径比 |
| がより大きく、画角がより大きい場合に優れた補正の可能性を提供するものです。 普通の |
| ガウス型と違ってこのレンズの前方の第一群は二枚のレンズからなっており、これによって |
| 収差補正の手段が更に追加されております。特に目立つことはすぐれた色収差補正で、 |
| 高次の色収差も認められない程度です。 その他の収差も極めて少量にとどまっています。 |
| レンズを絞ると鮮鋭度は急速に増大し、絞り5,6付近で最大値に達します。ズミターにおい |
| て特に価値のあることはその口径食(画面の周辺に向って像が暗くなること)を非常に軽減 |
| してあることで、これは特にカラー写真を撮影する場合に根本的に重要な意義をもつ事です。 |
| 白黒写真では露出寛容度が大きいためにレンズの口径食というものは一般にそれほど |
| めざわりにはなりません。ところがカラーフィルムでは、その露出寛容度が本質的に小さい |
| ものですから、レンズの口径食のある結果は画面周辺部の露出不足となり、この部分に |
| 非常にめざわりな不正な色の現われということになるのです。このような場合、この不愉快 |
| な現象を有効に防ぐには、レンズの前玉を比口径で定まる大きさよりもずっと大きくするの |
| が一法で、ズミターにおいてはこれが実行されており、類似のレンズにくらべ異常に大きな |
| トツプレンズがすぐ眼につく特微です。 これにより画面のヘリの方に達する斜めの光線束 |
| の断面積が、したがって光束の値が、本質的に大きくなり、その結果口径食が目立たぬ |
| 程度におさえられています。 この状況は上図に示す如く、斜めの光線束の中で、 |
| ハツチングをつけた部分はレンズを大きくすることによって得られた子午面内における増し |
| 分を示し、又これに対応する空間的な光線束の増し分は入射瞳の図のようになります。 |
| レンズの設計と計算に当っては、収差の補正と口径食との間に常に実用的な妥協が行わ |
| れるべきものですが、ちょうど上記のような場合(カラーフイルムの場合)には口径食の方 |
| に、重点が置かれなければなりません。 ズミターはこの点に関しては極めて好都合な |
| 妥協的解決法を見出されていると言うべきで、このレンズは、特にカラー写真を考えた場合 |
| に、あらゆる小型カメラ用レンズ中で卓越した地位を確保するものです。 |
| ズマリツト f=5cm 1:1.5 |
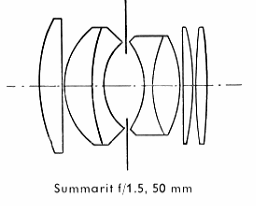 |
| 超大口径レンズ、ズマリツトは7枚構成レンズでガウス型の類別に属し、明るさという目的に |
| 対して特に好都合な補正の可能性を持つものです。 色収差の補正はすぐれており、像の |
| コントラストも優秀で、絞り開放においてすでに画面全体にわたり極めて鮮鋭です。少し絞っ |
| ただけで全般の鮮鋭度は増加し、絞り4でまれに見る高度のコントラストと解像力に達します |
| 画面全体にわたって光量分布が一様であること、ならびに歪曲収差のないことは、このよう |
| な大口径レンズとしては特に注目に値することです。 これはすぐれた性能を持つ、特に優れ |
| たレンズ構造であって、この種の小型カメラ用レンズとしては、まれにしか見当らないものです |
| ズマロン f=3・5cm 1:3.5 |
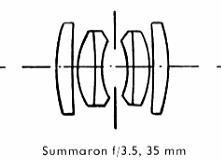 |
| 広角レンズ群に属するものに、画角64°を持つこのレンズもまたガウスが形の類別に属す |
| る物で6枚のレンズによりなり、その中の2枚は独立し、残りの4枚は接合されて二群になっ |
| ています。 広角レンズにおいては、口径食というものは画角が増すに従ってその弊害が |
| 目立って来る物です、この口径食が容認出来る程度におさえてあるかどうかと言うことに |
| 注意しなければなりません。 このズマロンにおいても前玉の大きさは比口径に相当する |
| 大きさよりもずっと大きく作られています。 その上更にこのレンズの後玉も又大きくなつて |
| おり、これにより斜めの光線束の断面積がさらに大きくなるようにしてます。 この両方の |
| 処置によって画面の周辺にも多量の光が到達し、そのため口径食が目立って妨害になる |
| と言う事はありません。 色収差の補正はこのレンズにおいては優れており、その他の |
| 諸収差も周到に補正されています。 それゆえ絞り開放においてすら結像の性能は注目 |
| すべき良さであります。 絞れば解像力とコントラストは上昇し絞り5・6と8の間で最高の |
| 要求に十分満足しえるような全画面にわたる鮮鋭さに到達します。 |
| へクトール f=2・8cm 1:6・3 |
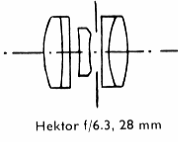 |
| 更に大きな76°と言う画角を持ったレンズとしてはへクトール2、8cmがあり、その構造は |
| 変形トリプレットであります。 このレンズの第一群と最後の群とはいずれもバルサム接合面 |
| を持っておりこれらは収差の補正と密接な関係を持っております。 このような広角レンズ |
| としては、1:6・3は明るいと見るべきですが、この開放絞りで、すでにライカ判全体を注目 |
| すべき鮮鋭度をもって描写し、しかも完全に歪曲がありません。 この極めて短焦点距離 |
| レンズとして特に注目に値することです。 このレンズは口径食を十分に小さくしたいと言う |
| 要求にこたえて、レンズの大きさを比口径に相応する大きさよりも大きくしてあります。 |
| 適当に絞るということは、広角レンズの場合、事情が許すならば常に推奨すべきことです、 |
| するとその結果画質は更に向上し、、(最小絞りは11) 画面全体に対する光量分布も |
| 改善されます。 |
| エルマー f= 9cm 1:4 |
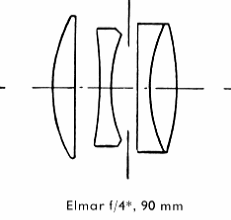 |
| エルマー9cm画角27°はエルマー50cmと同じ形式に属します、エルマー50cmの所で、 |
| 補正条件と最適鮮鋭度について言った事は、ここでもそのままなり立ちます。 特に言って |
| おきたいのはこのレンズにおいて口径食が非常に少ないことです。 このレンズは特に肖像 |
| 写真に適当していますが、風景写真にも、又他のすべての目的にも、焦点距離の長いことが |
| 求められる場合に使用すれば最良の結果が得られます。 |
| へクトール f= 13,5cm 1:4,5 |
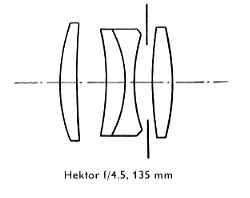 |
| へクトールf=13,5cm画角18°はその構造において変形トリプレットであり、その中央群 |
| に一つ集光性バルサム面が用いられています。 このバルサム面によって重要な収差補正 |
| の可能性が追加され、そしてこの可能性はこのレンズにおいて周到に利用しつくされていま |
| す。 そのため一般的の補正状態は優秀であり、これに応じて結像性能は他に越えて優れ |
| ています 。最高の解像力と最良のコントラストと互いにこのレンズを最も細かなティテール |
| を最も鮮鋭に描出する事が要求されるような撮影に特に合うところが特微でります。 |
| このレンズは開放においてすでに最良の結像性能を持っているので、焦点深度を大きくした |
| いと言う場合以外には、絞る必要はありません。 |
| テリート f=20cm 1:4,5 |
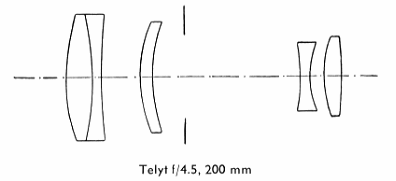 |
| テリートf=20cm画角12°その構造は望遠写真係で集光作用を持つ前玉群と発散作用を |
| 持つ、後玉群とが大きな間隔をへだてて対立した形式です。 このような構像の利益は像側 |
| のバックフォーカス、すなわち最後のレンズ面の頂点から焦点までの距離が、通常のレンズ |
| のバックフォーカスより本質的に小さいこと、比較的長い焦点距離に対し、レンズの前玉から |
| マウント面まで全長が比較的短く、したがって持ちあつかい易い結果になります。全般的の |
| 補正は極めて良好であり、特に色収差補正の徹底していることと歪曲収差の全然ない事は |
| 注目に値します。 |
※ 上記の文章を書籍・webページ上で無断使用する事を禁じます。